本节为“过程能力”平台中使用的分布提供密度函数 f,同时还为除 Johnson 分布之外的所有分布提供期望值和方差。
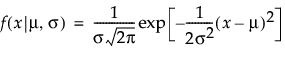 ,
, 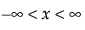 ,
, 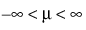 , σ > 0
, σ > 0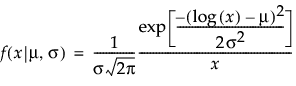 , x > 0,
, x > 0, 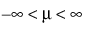 , σ > 0
, σ > 0其中,μi、σi 和 πi 分别是第 i 个组的均值、标准差和比例,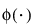 是标准正态概率密度函数。对于“两正态混合”,k 等于 2。对于“三正态混合”分布,k 等于 3。为混合中的每个组估计单独的均值、标准差和占总体的比例。
是标准正态概率密度函数。对于“两正态混合”,k 等于 2。对于“三正态混合”分布,k 等于 3。为混合中的每个组估计单独的均值、标准差和占总体的比例。
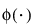 是标准正态概率密度函数。对于“两正态混合”,k 等于 2。对于“三正态混合”分布,k 等于 3。为混合中的每个组估计单独的均值、标准差和占总体的比例。
是标准正态概率密度函数。对于“两正态混合”,k 等于 2。对于“三正态混合”分布,k 等于 3。为混合中的每个组估计单独的均值、标准差和占总体的比例。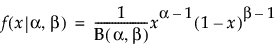 ,
, 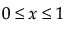 ,
, 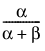
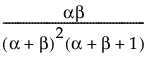
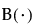 是 Beta 函数。
是 Beta 函数。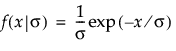 ,
, 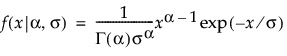 ,
, 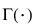 是 gamma 函数。
是 gamma 函数。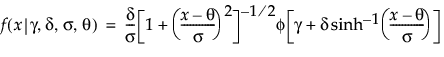 ,
, 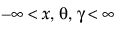 ,
, 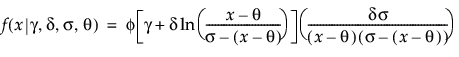 ,
, 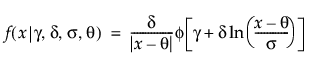 ,适用于:
,适用于: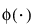 是标准正态概率密度函数。
是标准正态概率密度函数。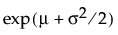
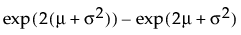
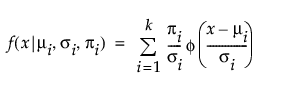
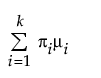
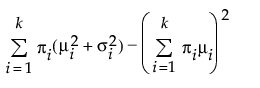
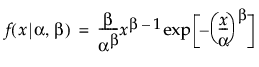 ,
, 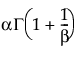
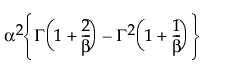
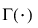 是 gamma 函数。
是 gamma 函数。