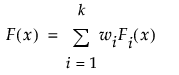可靠性和生存方法 • 寿命分布 • “寿命分布”报表选项 • 混合
上一个
 • 
下一个
混合
“拟合混合模型”选项将在报表中添加“混合”分级显示项，您可以在其中拟合数据的混合分布。
混合分布的概率函数 F(x) 定义如下：
其中，Fi(x) 是受支持的分布之一，k 是混合模型中的成分个数，wi 是总和为 1 的正权重。“拟合混合模型”选项尝试标识从每个成分分布 Fi(x) 中抽取的观测聚类。它估计混合模型的参数以及从任意给定成分中抽取观测的概率。
模型拟合和混合起始值方法
拟合方法基于有关相应聚类的假设，该方法称为“起始值方法”。假定您指定了 k 个分布。有三种“起始值方法”：
•
“单个聚类”假定所有观测在一定程度上都受到所有成分分布的影响。没有任何密度单独影响一部分观测。
•
“可分隔的聚类”假定成分分布对某些观测的影响比对其他观测更深。对于可分隔的聚类，k 个密度中的每一个都具有可标识的模式并定义一个聚类。
•
“重叠聚类”假定了介于“单个聚类”与“可分隔的聚类”之间的一种情形。某些密度单独影响部分观测，但其他密度联合影响部分观测。在这种情况下，数据中有 m 个聚类，其中 m 小于 k（总密度数）。
拟合过程包含以下步骤：
1.
定义观测聚类。
2.
基于“起始值方法”将聚类分配到密度：
‒
对于“可分隔的聚类”，分配给指定的成分密度的最高似然聚类通过检查可能的排列来确定。
‒
对于“重叠聚类”，分配给指定的成分密度的最高似然聚类通过检查可能的聚类排列和观测组合来确定。
注意：假定您使用给定的“起始值方法”拟合了某个模型，然后又选择了另一种“起始值方法”。若无法基于似然值实现更好的拟合，则不添加任何新模型。
“混合”控制面板
该控制面板包含以下项：
成分
列出您可以用作拟合混合分布的成分的分布。
数量
选择混合分布中具有给定分布的成分个数。“数量”值的总和为 k，即混合分布中密度的个数。
起始值方法
选择反映您关于混合分布的假设的方法。请参见模型拟合和混合起始值方法。
叠加
显示未删失数据值的非参数估计值 (Kaplan-Meier-Turnbull)。拟合混合模型时，该图会随之更新以显示模型和 95% 水平置信带。置信带不受“寿命分布”红色小三角菜单中的“更改置信水平”选项的影响。“图例”显示在图右侧。
执行
点击执行可拟合所需的混合模型。“模型列表”会随您拟合的模型更新，同时添加具有混合模型名称的报表。
“拟合混合模型”报表
模型列表
“模型列表”报表会列出您拟合的混合分布。该报表提供每个混合分布的参数数目、实际观测数，以及 AICc、-2*对数似然和 BIC 统计量。有关这些统计量的更多详细信息，请参见《拟合线性模型》手册中的“似然、AICc 和 BIC”。
请注意以下事项：
•
以上每个统计量的值越小指示拟合效果越好。
•
各行按 AICc 排序。
•
比较准则红色小三角选项不影响“模型列表”中模型的顺序。
•
AICc、-2*对数似然和 BIC 统计量还显示在“模型比较”表中。这样您就可以将混合分布与您的数据的其他分布进行比较。请参见模型比较。
“混合模型”报表
“模型列表”报表之后跟有您已经拟合的每个混合分布的报表。每个报表的标题使用指定的成分及其数量描述对应的混合模型。报表会列出参数、参数估计值、标准误差和 95% Wald 置信区间。在启动窗口中将“似然”选作“置信区间方法”并不会影响这些区间。
为混合模型中的每个分布提供了参数估计值。“参数”列还包括名为“对应部分 <i>”的参数，其中 i = 1, 2, .., k-1。这些是混合模型的权重 wi 的估计值。由于这些权重的总和为 1，所以可以根据前 k - 1 个权重计算出第 k 个权重。
“密度叠加”图
“密度叠加”图显示混合模型中每个成分的密度函数的估计值。图右侧的图例支持您选择要显示的密度函数。
“混合模型”报表选项
该红色小三角菜单包含以下选项：
删除
删除模型报表以及“模型列表”中该模型对应的条目。
显示刻画器
显示混合分布 F 的四种刻画器。有关这些刻画器的红色小三角选项的说明，请参见混合模型刻画器选项。
‒
“分布刻画器”显示作为时间的函数的累积失效概率。
‒
“分位数刻画器”显示作为累积概率的函数的失效时间。
‒
“危险率刻画器”显示作为时间的函数的危险率。
‒
“密度刻画器”显示分布的密度函数。
保存预测
对于每个混合模型密度，会在数据表中保存一列，其中包含某个观测属于该密度的概率。对于计算中使用的公式，请参见“拟合混合模型”保存预测公式。
混合模型刻画器选项
每个混合模型报表的刻画器都包含以下红色小三角选项：
置信区间
“分布”、“分位数”和“危险率”刻画器显示所绘函数的基于 Wald 的 95% 置信曲线。该选项显示或隐藏置信曲线。当您从“寿命分布”红色小三角菜单中选择“更改置信水平”时，置信水平不受影响。
注意：为了减少计算时间，刻画器中提供的置信区间基于 Wald 方法，即便您在启动窗口中将“似然”选作“置信区间方法”也是如此。
重置因子网格
为每个因子显示一个窗口，允许您为因子的当前设置输入特定值，锁定该设置，以及控制网格的各个方面。详细信息，请参见《刻画器指南》手册中的“重置因子网格”。
因子设置
提供一个菜单，其中包含与刻画器设置、脚本和关联刻画器相关的选项。详细信息，请参见《刻画器指南》手册中的“因子设置”。
拟合混合模型的示例
在本例中，您拟合两个混合分布，然后标识属于第二个混合分布的其中一个聚类的观测。
拟合两个混合分布
1.
选择帮助 > 样本数据库，然后打开 Reliability/Mixture Demo.jmp。
2.
选择分析 > 可靠性和生存 > 寿命分布。
3.
选择 Y1 并点击 Y，事件时间。
4.
点击确定。
5.
从“寿命分布”旁边的红色小三角菜单中选择拟合混合模型。
6.
在 Weibull 旁边的数量框中键入 2。
7.
在“起始值方法”面板中选择可分隔的聚类。
8.
点击执行。
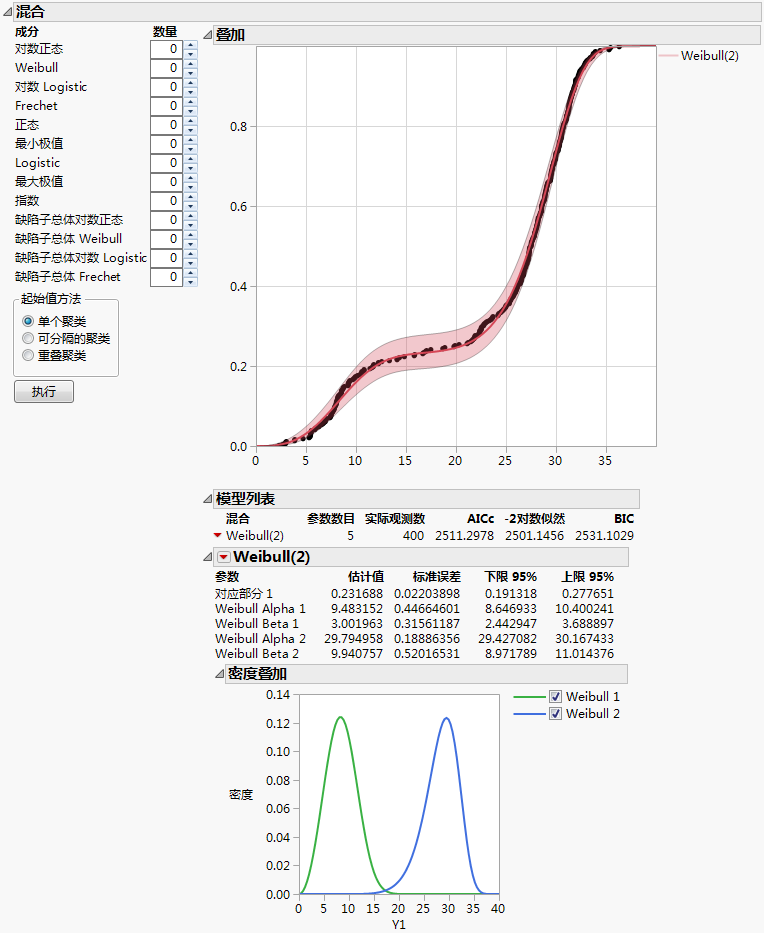
图 3.10 拟合“Weibull(2)”的混合模型
JMP 拟合包含两个 Weibull 成分的混合模型。“对应部分 1”的估计值为 0.231688，指示大约有 23% 的观测服从 Weibull 分布，其 alpha = 9.483152，beta = 3.001962。剩余的 77% 估计来自第二个 Weibull 分布。
为了将该模型与另一个模型进行比较，您可以更改“成分”选择和成分“数量”。
9.
在对数正态旁边键入 1，并且在 Weibull 旁边键入 1。
10.
点击执行。
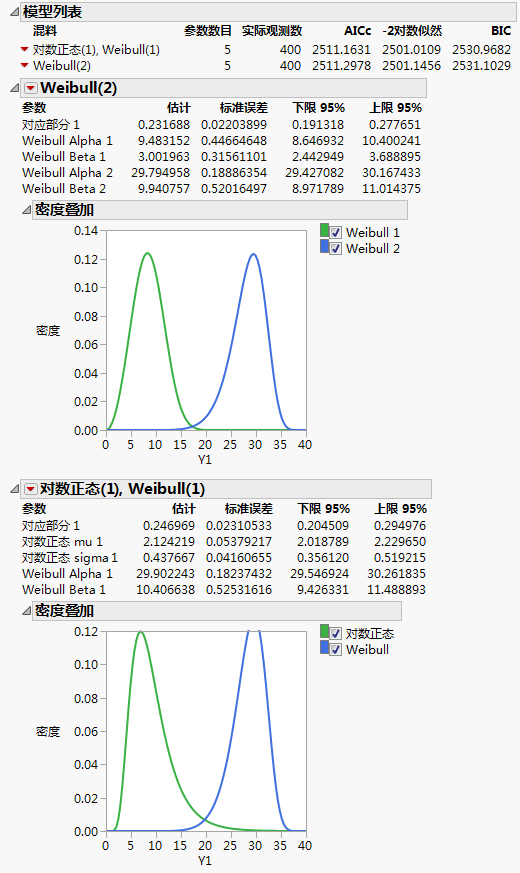
图 3.11 拟合“对数正态(1)，Weibull(1)”的混合模型
“叠加”图随之更新以显示两个混合模型。“模型列表”中的图和统计量指出“对数正态(1)，Weibull(1)”混合模型看起来提供了与“Weibull(2)”混合模型极为相似的拟合。
标识属于某聚类的观测
1.
从“对数正态(1)，Weibull(1)”红色小三角菜单中，选择保存预测。
将向数据表添加两列：
‒
对数正态(1)，Weibull(1) - 以下成分的预测概率: 对数正态
‒
对数正态(1)，Weibull(1) - 以下成分的预测概率: Weibull
2.
选择分析 > 分布。
3.
从“选择列”列表中选择这两个新列，然后点击 Y，列。
4.
选中仅显示直方图。
5.
点击确定。
6.
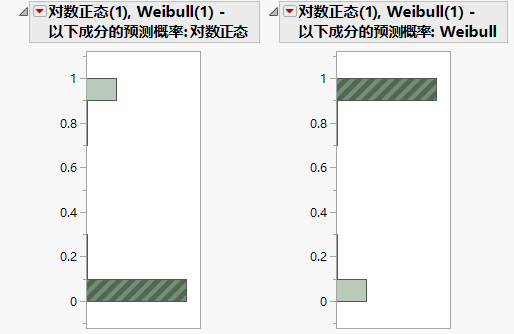
在对数正态(1)，Weibull(1) - 以下成分的预测概率: Weibull 的直方图中，点击与接近 1 的值对应的直条。
图 3.12 混合概率的直方图
在数据表中，选定了 297 个对应的行。这些是可能来自参数 alpha = 29.90 且 beta = 10.41 的 Weibull 分布的观测。