图 13.5 指数、Weibull 和对数正态图以及报表
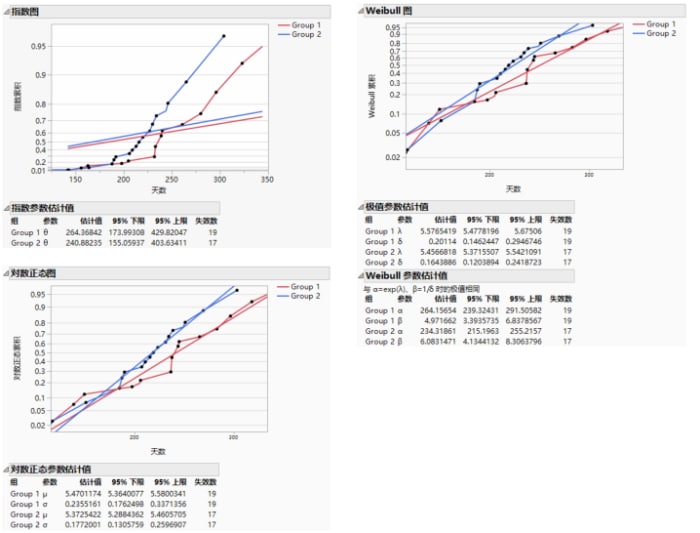
Weibull 分布是用于对事件时间数据建模的最常用的分布。Weibull 分布可有两个或三个参数。“生存”平台拟合两参数 Weibull 分布。不同作者有很多不同方式来参数化该分布（如依照 JMP 的 alpha 和 beta 的各种 Weibull 参数中所示）。JMP 报告其中两种参数化：Weibull alpha-beta 参数化和基于最小极值分布的参数化。
alpha-beta 参数化（显示在“Weibull 参数估计值”报表中），在可靠性文献 (Nelson 1990) 中广泛使用。将 alpha 解释为 63.2% 的单元失效时的分位数。beta 参数确定危险率如何随时间变化。若 beta > 1，危险率将随时间提高；若 beta < 1，则危险率随时间下降；若beta = 1，则危险率不随时间变化。危险率函数为常数的 Weibull 分布等同于指数分布。
lambda-delta 极值参数化显示在“极值参数估计值”报表中。该参数化有时在统计意义上是需要的，因为它将 Weibull 分布置于位置-尺度的设置中 (Meeker and Escobar 1998, p. 86)。位置参数为 lambda，尺度参数为 delta。与 alpha-beta 参数化相关的是，lambda 等于 alpha 的自然对数，delta 等于 beta 的倒数。因此，delta 参数确定危险率如何随时间变化。若 delta > 1，危险率将随时间降低；若 delta < 1，则危险率随时间提高；若delta = 1，则危险率不随时间变化。危险率函数为常数的 Weibull 分布等同于指数分布。
|
alpha=alpha
|
beta=beta
|
|
|
eta=alpha
|
beta=beta
|
|
|
c = alpha
|
m = beta
|
|
|
eta=alpha
|
beta=beta
|
|
|
exp(X beta)=alpha
|
lambda=beta
|
|
|
beta=alpha
|
alpha=beta
|
|
|
lambda = 1/alpha
|
p = beta
|
|
|
lambda=log(alpha)
|
delta=1/beta
|
|
|
mu=log(alpha)
|
sigma=1/beta
|
对数正态分布也是极常用的用于对事件时间数据建模的分布。对数正态分布等同于对值取对数后服从的正态分布。若您要拟合数据的正态分布，可以取它的 exp() 并使用对数正态分布对数据建模。请参见“拟合参数生存”一章中第 330 页的“拟合参数生存的更多示例”。
要查看指数、Weibull 和对数正态拟合的其他选项，请按住 Shift 键，点击乘积限生存拟合菜单的红色小三角菜单，然后点击所需的拟合。
图 13.6 置信等高线图
在拟合相应分布时，JMP 可以约束 Theta（指数）、Beta (Weibull) 和 Sigma（对数正态）参数的值。在 WeiBayes 情形中需要该功能，例如：