您可以创建公式,这些公式通过在指定的分布约束内高效“掷骰子”来生成实数。每次在“公式编辑器”窗口中点击应用时,这些函数生成一组新的随机数。
注意:使用 Mersenne-Twister 方法生成随机数。此方法具有长度为 219937-1 的期间。有关生成程序的详细信息,请参见 Matsumoto 和 Nishimura (1998)。这些新的生成程序已被验证通过了 Marshalled (1996) 中所述的所有 DIEHARD 检验。
生成均匀介于 0 到 1 之间的随机数,这意味着介于 0 到 1 之间的任意数与生成的任何其他数的可能性相同。结果近似均匀分布。您可以平移分布并使用常数更改其范围。例如,5 + Random Uniform()*20 生成介于 5 到 25 的均匀随机数。
生成近似均值为 0、标准差为 1 的正态分布的随机数(若未使用参数),否则生成您输入的参数作为均值和标准差的近似正态分布的随机数。正态分布为对称的钟形。若未输入参数,还可以使用常数修改 Random Normal 函数,以获得具有特定均值和标准差的正态分布。例如,公式 Random Normal()*5 + 30 生成均值为 30、标准差为 5 的随机正态变量。
例如,Random Exp()*.1 生成 lambda=0.1 的指数分布。指数分布通常用于为简单的失效时间数据建模,其中 lambda 为失效率。
对您作为函数参数输入的参数 alpha 生成 gamma 分布。gamma 分布描述直到事件第 k 次出现的时间。gamma 分布还可以有尺度参数 beta。可以使用公式 beta*Random Gamma(alpha) 生成具有形状参数 alpha 和尺度 beta 的 gamma 变元。若 2*alpha 是整数,则使用公式 2*Random Gamma(alpha) 生成自由度为 2*alpha 的卡方变元。
生成位置参数为 0、尺度参数为 1 的 Cauchy 分布。Cauchy 分布为对称钟形,但是比正态分布有更厚的尾部。可以使用公式 alpha+beta*Random Cauchy() 生成位置参数为 alpha、尺度参数为 beta 的 Cauchy 变元。
根据交替的概率和结果表达式生成随机类别(例如,Random Category(.2, "A", .3, "B", .4, "C", "D");))。
生成从 1 到作为 n1 输入的参数(若没有输入 n2 的值)的整数的均匀分布。若同时输入 n1 和 n2 (n1<n2),Random Integer 将生成从 n1 到 n2(包括端点)的整数的均匀分布。
生成包含您作为函数参数输入的参数的二项分布的随机数。第一个参数为 n,即二项实验中的试验次数。第二个参数为 p,即发生关注事件的概率。n 为 1 时,二项函数生成 Bernoulli 试验分布。例如,n =1 且 p = 0.5 得到投硬币的分布。二项分布的均值为 np,方差为 np(1 – p)。
生成作为函数参数输入的参数的负二项分布。第一个参数是关注的成功次数 (r),第二个参数是成功概率 (p)。关注的随机变量是第 r 次成功前的失败次数。二项变元的试验次数是固定的而成功次数是变量,负二项变元则针对固定的成功次数和随机的试验次数。负二项分布的均值为 (r(1 – p))/p,方差为 (r(1 – p))/p2。
返回包含作为函数参数输入的参数的几何分布的随机数。参数 p 为特定事件在任意一次试验中出现的概率。特定事件第一次出现所经历的试验次数由几何分布描述。几何分布的均值为 (1-p)/p,方差为 (1 – p)/p2。
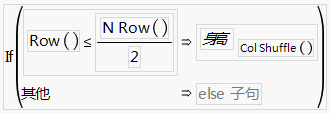
图 A.16 标识 50% 随机样本的公式
生成有放回的频数统计的随机选择,适用于 Bootstrapping。例如,它支持第二个 Freq Column 参数,以便执行 Bootstrap 样本,这些样本与在第二个参数中指定的预先存在的频数列有关。Resample Freq() 生成 100% 再抽样。ResampleFreq(rate) 生成 rate 频数样本。Resample(rate, column) 生成由该比率乘以指定列之和所得到的样本。