Fit StatisticsThe Fit Statistics report gives statistics used for model comparison. For all fit statistics, smaller is better. A likelihood ratio test between two models can be performed if one model is contained within the other. If not, a cautious comparison of likelihoods can be informative. For an example, see Fit a Spatial Structure Model.
Description of the Fit Statistics Report uses the following notation:
Here y is the nx1 vector of observations,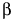 
is a vector of fixed-effect parameters, γ is a vector of random-effect parameters, and ε is a vector of errors.
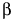is a vector of fixed-effect parameters, γ is a vector of random-effect parameters, and ε is a vector of errors.|
•
|
|
•
|
With these assumptions, the variance of y is given as follows:
|
and p is the rank of X. Use the residual likelihood only for model comparisons where the fixed effects portion of the model is identical. For more details, see Likelihood, AICc, and BIC in Statistical Details.
The evaluation of twice the negative log likelihood function. For more details, see Likelihood, AICc, and BIC in Statistical Details.
Corrected Akaike’s Information Criterion. For more details, see Likelihood, AICc, and BIC in Statistical Details.
Bayesian Information Criterion. For more details, see Likelihood, AICc, and BIC in Statistical Details.
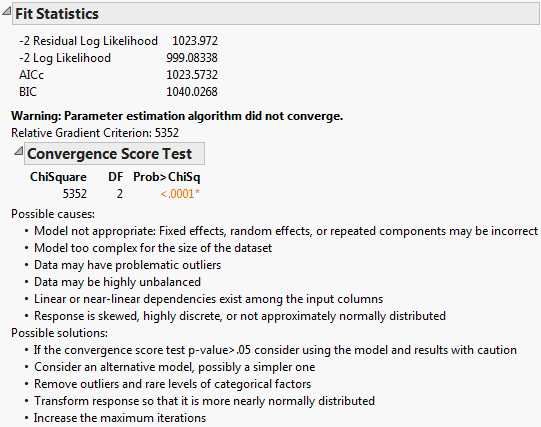
Convergence Score TestIf there are problems with model convergence, a warning message is displayed below the fit statistics. Figure 7.11 shows the warning that suggests the cause and possible solutions to the convergence issue. It also includes a test of the relative gradient at the final iteration. If this test is non-significant, the model might be correct but not fully reaching the convergence criteria. In this case, consider using the model and results with caution. For more information, see Convergence Score Test.
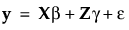
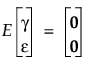
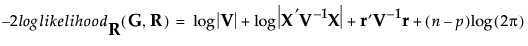
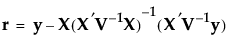
Figure 7.11 Convergence Score Test
