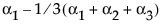Nominal Factors

Nominal factors are transformed into indicator variables for the design matrix. SAS GLM constructs an indicator column for each nominal level. JMP constructs the same indicator columns for each nominal level except the last level. When the last nominal level occurs, a one is subtracted from all the other columns of the factor. For example, consider a nominal factor A with three levels coded for GLM and for JMP as shown below.

Table 12.1 Nominal Factor A
	GLM			JMP
A	A1	A2	A3	A13	A23
A1	1	0	0	1	0
A2	0	1	0	0	1
A3	0	0	1	–1	–1

In GLM, the linear model design matrix has linear dependencies among the columns, and the least squares solution uses a generalized inverse. The solution chosen happens to be such that the A3 parameter is set to zero.

In JMP, the linear model design matrix is coded so that it achieves full rank unless there are missing cells or other incidental collinearity. The parameter for the A effect for the last level is the negative sum of the other levels, which makes the parameters sum to zero over all the effect levels.

Interpretation of Parameters

Note: The parameter for a nominal level is interpreted as the differences in the predicted response for that level from the average predicted response over all levels.

The design column for a factor level is constructed as the zero-one indicator of that factor level minus the indicator of the last level. This is the coding that leads to the parameter interpretation above.

Table 12.2 Interpreting Parameters
JMP Parameter Report	How to Interpret	Design Column Coding
Intercept	mean over all levels	1´
A[1]		(A==1) – (A==3)
A[2]		(A==2) – (A==3)

Interactions and Crossed Effects

Interaction effects with both GLM and JMP are constructed by taking a direct product over the rows of the design columns of the factors being crossed. For example, the GLM code

PROC GLM;

	CLASS A B;

	MODEL A B A*B;

yields this design matrix:

Table 12.3 Design Matrix
		A			B			AB
A	B	1	2	3	1	2	3	11	12	13	21	22	23	31	32	33
A1	B1	1	0	0	1	0	0	1	0	0	0	0	0	0	0	0
A1	B2	1	0	0	0	1	0	0	1	0	0	0	0	0	0	0
A1	B3	1	0	0	0	0	1	0	0	1	0	0	0	0	0	0
A2	B1	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0
A2	B2	0	1	0	0	1	0	0	0	0	0	1	0	0	0	0
A2	B3	0	1	0	0	0	1	0	0	0	0	0	1	0	0	0
A3	B1	0	0	1	1	0	0	0	0	0	0	0	0	1	0	0
A3	B2	0	0	1	0	1	0	0	0	0	0	0	0	0	1	0
A3	B3	0	0	1	0	0	1	0	0	0	0	0	0	0	0	1

Using the JMP Fit Model command and requesting a factorial model for columns A and B produces the following design matrix. Note that A13 in this matrix is A1–A3 in the previous matrix. However, A13B13 is A13*B13 in the current matrix.

Table 12.4 Current Matrix
		A		B
A	B	13	23	13	23	A13 B13	A13 B23	A23 B13	A23 B23
A1	B1	1	0	1	0	1	0	0	0
A1	B2	1	0	0	1	0	1	0	0
A1	B3	1	0	–1	–1	–1	–1	0	0
A2	B1	0	1	1	0	0	0	1	0
A2	B2	0	1	0	1	0	0	0	1
A2	B3	0	1	–1	–1	0	0	–1	–1
A3	B1	–1	–1	1	0	–1	0	–1	0
A3	B2	–1	–1	0	1	0	–1	0	–1
A3	B3	–1	–1	–1	–1	1	1	1	1

The JMP coding saves memory and some computing time for problems with interactions of factors with few levels.

The expected values of the cells in terms of the parameters for a three-by-three crossed model are:

Table 12.5 Three-by-Three Crossed Model
	B1	B2	B3
A1
A2
A3

Nested Effects

Nested effects in GLM are coded the same as interaction effects because GLM determines the right test by what is not in the model. Any effect not included in the model can have its effect soaked up by a containing interaction (or, equivalently, nested) effect.

Nested effects in JMP are coded differently. JMP uses the terms inside the parentheses as grouping terms for each group. For each combination of levels of the nesting terms, JMP constructs the effect on the outside of the parentheses. The levels of the outside term do not need to line up across the levels of the nesting terms. Each level of nest is considered separately with regard to the construction of design columns and parameters.

Table 12.6 Nested Effects
				B(A)
				A1	A1	A2	A2	A3	A3
A	B	A13	A23	B13	B23	B13	B23	B13	B23
A1	B1	1	0	1	0	0	0	0	0
A1	B2	1	0	0	1	0	0	0	0
A1	B3	1	0	–1	–1	0	0	0	0
A2	B1	0	1	0	0	1	0	0	0
A2	B2	0	1	0	0	0	1	0	0
A2	B3	0	1	0	0	–1	–1	0	0
A3	B1	–1	–1	0	0	0	0	1	0
A3	B2	–1	–1	0	0	0	0	0	1
A3	B3	–1	–1	0	0	0	0	–1	–1

Least Squares Means across Nominal Factors

Least squares means are the predicted values corresponding to some combination of levels, after setting all the other factors to some neutral value. The neutral value for direct continuous regressors is defined as the sample mean. The neutral value for an effect with uninvolved nominal factors is defined as the average effect taken over the levels (which happens to result in all zeros in our coding). Ordinal factors use a different neutral value in Ordinal Least Squares Means. The least squares means might not be estimable, and if not, they are marked nonestimable. The least squares means in JMP agree with those in SAS PROC GLM (Goodnight and Harvey 1978) in all cases except when a weight is used. When a weight variable is used, JMP uses a weighted mean and SAS PROC GLM uses an unweighted mean for its neutral values.

Effective Hypothesis Tests

Generally, the hypothesis tests produced by JMP agree with the hypothesis tests of most other trusted programs, such as SAS PROC GLM (Hypothesis types III and IV). The following two sections describe where there are differences.

In SAS PROC GLM, the hypothesis tests for Types III and IV are constructed using the general form of estimable functions and finding functions that involve only the effects of interest and effects contained by the effects of interest (Goodnight 1978).

The same tests are constructed in JMP. However, because there is a different parameterization, an effect can be tested (assuming full rank for now) by doing a joint test on all the parameters for that effect. The tests do not involve containing interaction parameters because the coding has made them uninvolved with the tests on their contained effects.

If there are missing cells or other singularities, the JMP tests are different from GLM tests. There are several ways to describe them:

•

JMP tests are equivalent to testing that the least squares means are different, at least for main effects. If the least squares means are nonestimable, then the test cannot include some comparisons and therefore loses degrees of freedom. For interactions, JMP is testing that the least squares means differ by more than just the marginal pattern described by the containing effects in the model.

•

JMP tests an effect by comparing the SSE for the model with that effect to the SSE for the model without that effect. This logic applies if there are no nested terms, which complicate the logic slightly. JMP parameterizes the model so that this method makes sense.

•

JMP implements the effective hypothesis tests described by Hocking (1985, pp. 80–89, 163–166), although JMP uses structural rather than cell-means parameterization. Effective hypothesis tests start with the hypothesis desired for the effect and include “as much as possible” of that test. Of course, if there are containing effects with missing cells, then this test has to drop part of the hypothesis because the complete hypothesis would not be estimable. The effective hypothesis drops as little of the complete hypothesis as possible.

•

The differences among hypothesis tests in JMP and GLM (and other programs) that relate to the presence of missing cells are not considered interesting tests anyway. If an interaction is significant, the test for the contained main effects is not interesting. If the interaction is not significant, then it can always be dropped from the model. Some tests are not even unique. If you relabel the levels in a missing cell design, then the GLM Type IV tests can change.

The following section continues this topic in finer detail.

Singularities and Missing Cells in Nominal Effects

Consider the case of linear dependencies among the design columns. With JMP coding, this does not occur unless there is insufficient data to fill out the combinations that need estimating, or unless there is some type of confounding or collinearity of the effects.

With linear dependencies, a least squares solution for the parameters might not be unique and some tests of hypotheses cannot be tested. The strategy chosen for JMP is to set parameter estimates to zero in sequence as their design columns are found to be linearly dependent on previous effects in the model. A special column in the report shows what parameter estimates are zeroed and which parameter estimates are estimable. A separate singularities report shows what the linear dependencies are.

In cases of singularities the hypotheses tested by JMP can differ from those selected by GLM. Generally, JMP finds fewer degrees of freedom to test than GLM because it holds its tests to a higher standard of marginality. In other words, JMP tests always correspond to tests across least squares means for that effect, but GLM tests do not always have this property.

For example, consider a two-way model with interaction and one missing cell where A has three levels, B has two levels, and the A3B2 cell is missing.

Table 12.7 Two-Way Model with Interaction
A B	A1	A2	B1	A1B1	A2B1
A1 B1	1	0	1	1	0
A2 B1	0	1	1	0	1
A3 B1	–1	–1	1	–1	–1
A1 B2	1	0	–1	–1	0
A2 B2	0	1	–1	0	–1
A3 B2	–1	–1	–1	1	1	Suppose this interaction is missing.

The expected values for each cell are:

Table 12.8 Expected Values
	B1	B2
A1
A2
A3

Obviously, any cell with data has an expectation that is estimable. The cell that is missing has an expectation that is nonestimable. In fact, its expectation is precisely that linear combination of the design columns that is in the singularity report

Suppose that you want to construct a test that compares the least squares means of B1 and B2. In this example, the average of the rows in the above table give these least squares means.

LSM(B1) =

LSM(B2) =

LSM(B1) – LSM(B2) =

Note that this shows that a test on the β1 parameter is equivalent to testing that the least squares means are the same. But because β1 is not estimable, the test is not testable, meaning there are no degrees of freedom for it.

Now, construct the test for the least squares means across the A levels.

Neither of these turn out to be estimable, but there is another comparison that is estimable; namely comparing the two A columns that have no missing cells.

LSM(A1) – LSM(A2) =

This combination is indeed tested by JMP using a test with 1 degree of freedom, although there are two parameters in the effect.

The estimability can be verified by taking its inner product with the singularity combination, and checking that it is zero:

Table 12.9 Verification
	singularity	combination
parameters	combination	to be tested
m	1	0
a1	–1	1
a2	–1	–1
b1	–1	0
ab11	1	0
ab21	1	0

It turns out that the design columns for missing cells for any interaction always knocks out degrees of freedom for the main effect (for nominal factors). Thus, there is a direct relation between the non-estimability of least squares means and the loss of degrees of freedom for testing the effect corresponding to these least squares means.

How does this compare with what GLM does? GLM and JMP do the same test when there are no missing cells. That is, they effectively test that the least squares means are equal. But when GLM encounters singularities, it focuses out these cells in different ways, depending on whether they are Type III or Type IV. For Type IV, it looks for estimable combinations that it can find. These might not be unique, and if you reorder the levels, you might get a different result. For Type III, it does some orthogonalization of the estimable functions to obtain a unique test. But the test might not be very interpretable in terms of the cell means.

The JMP approach has several points in its favor, although at first it might seem distressing that you might lose more degrees of freedom than with GLM:

The tests are philosophically linked to LSMs.

The tests are easy computationally, using reduction sum of squares for reparameterized models.

The tests agree with Hocking’s “Effective Hypothesis Tests”.

The tests are whole marginal tests, meaning they always go completely across other effects in interactions.

The last point needs some elaboration: Consider a graph of the expected values of the cell means in the previous example with a missing cell for A3B2.

Figure 12.1 Expected Values of the Cell Means

The graph shows expected cell means with a missing cell. The means of the A1 and A2 cells are profiled across the B levels. The JMP approach says you cannot test the B main effect with a missing A3B2 cell, because the mean of the missing cell could be anything, as allowed by the interaction term. If the mean of the missing cell were the higher value shown, the B effect would likely test significant. If it were the lower, it would likely test nonsignificant. The point is that you do not know. That is what the least squares means are saying when they are declared nonestimable. That is what the hypotheses for the effects should be saying too—that you do not know.

If you want to test hypotheses involving margins for subsets of cells, then that is what GLM Type IV does. In JMP, you would have to construct these tests yourself by partitioning the effects with a lot of calculations or by using contrasts.

JMP and GLM Hypotheses

GLM works differently than JMP and produces different hypothesis tests in situations where there are missing cells. In particular, GLM does not recognize any difference between a nesting and a crossing in an effect, but JMP does. Suppose that you have a three-layer nesting of A, B(A), and C(A B) with different numbers of levels as you go down the nested design.

Table 12.10, shows the test of the main effect A in terms of the GLM parameters. The first set of columns is the test done by JMP. The second set of columns is the test done by GLM Type IV. The third set of columns is the test equivalent to that by JMP; it is the first two columns that have been multiplied by a matrix:

to be comparable to the GLM test. The last set of columns is the GLM Type III test. The difference is in how the test distributes across the containing effects. In JMP, it seems more top-down hierarchical. In GLM Type IV, the test seems more bottom-up. In practice, the test statistics are often similar.

Table 12.10 Comparison of GLM and JMP Hypotheses
Parameter	JMP Test for A		GLM-IV Test for A		JMP Rotated Test		GLM-III Test for A
u	0	0	0	0	0	0	0	0
a1	0.6667	-0.3333	1	0	1	0	1	0
a2	–0.3333	0.6667	0	1	0	1	0	1
a3	–0.3333	-0.3333	-1	-1	-1	-1	-1	-1

a1b1	0.1667	-0.0833	0.2222	0	0.25	0	0.2424	0
a1b2	0.1667	-0.0833	0.3333	0	0.25	0	0.2727	0
a1b3	0.1667	-0.0833	0.2222	0	0.25	0	0.2424	0
a1b4	0.1667	-0.0833	0.2222	0	0.25	0	0.2424	0

a2b1	-0.1667	0.3333	0	0.5	0	0.5	0	.5
a2b2	-0.1667	0.3333	0	0.5	0	0.5	0	.5

a3b1	-0.1111	-0.1111	-0.3333	-0.3333	-0.3333	-0.3333	-0.3333	-0.3333
a3b2	-0.1111	-0.1111	-0.3333	-0.3333	-0.3333	-0.3333	-0.3333	-0.3333
a3b3	-0.1111	-0.1111	-0.3333	-0.3333	-0.3333	-0.3333	-0.3333	-0.3333

a1b1c1	0.0833	-0.0417	0.1111	0	0.125	0	0.1212	0
a1b1c2	0.0833	-0.0417	0.1111	0	0.125	0	0.1212	0
a1b2c1	0.0556	-0.0278	0.1111	0	0.0833	0	0.0909	0
a1b2c2	0.0556	-0.0278	0.1111	0	0.0833	0	0.0909	0
a1b2c3	0.0556	-0.0278	0.1111	0	0.0833	0	0.0909	0
a1b3c1	0.0833	-0.0417	0.1111	0	0.125	0	0.1212	0
a1b3c2	0.0833	-0.0417	0.1111	0	0.125	0	0.1212	0
a1b4c1	0.0833	-0.0417	0.1111	0	0.125	0	0.1212	0
a1b4c2	0.0833	-0.0417	0.1111	0	0.125	0	0.1212	0

a2b1c1	-0.0833	0.1667	0	0.25	0	0.25	0	0.25
a2b1c2	-0.0833	0.1667	0	0.25	0	0.25	0	0.25
a2b2c1	-0.0833	0.1667	0	0.25	0	0.25	0	0.25
a2b2c2	-0.0833	0.1667	0	0.25	0	0.25	0	0.25

a3b1c1	-0.0556	-0.0556	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667
a3b1c2	-0.0556	-0.0556	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667
a3b2c1	-0.0556	-0.0556	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667
a3b2c2	-0.0556	-0.0556	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667
a3b3c1	-0.0556	-0.0556	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667
a3b3c2	-0.0556	-0.0556	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667	-0.1667

		A			B			AB
A	B	1	2	3	1	2	3	11	12	13	21	22	23	31	32	33
A1	B1	1	0	0	1	0	0	1	0	0	0	0	0	0	0	0
A1	B2	1	0	0	0	1	0	0	1	0	0	0	0	0	0	0
A1	B3	1	0	0	0	0	1	0	0	1	0	0	0	0	0	0
A2	B1	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0
A2	B2	0	1	0	0	1	0	0	0	0	0	1	0	0	0	0
A2	B3	0	1	0	0	0	1	0	0	0	0	0	1	0	0	0
A3	B1	0	0	1	1	0	0	0	0	0	0	0	0	1	0	0
A3	B2	0	0	1	0	1	0	0	0	0	0	0	0	0	1	0
A3	B3	0	0	1	0	0	1	0	0	0	0	0	0	0	0	1

		A			B			AB
A	B	1	2	3	1	2	3	11	12	13	21	22	23	31	32	33
A1	B1	1	0	0	1	0	0	1	0	0	0	0	0	0	0	0
A1	B2	1	0	0	0	1	0	0	1	0	0	0	0	0	0	0
A1	B3	1	0	0	0	0	1	0	0	1	0	0	0	0	0	0
A2	B1	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0
A2	B2	0	1	0	0	1	0	0	0	0	0	1	0	0	0	0
A2	B3	0	1	0	0	0	1	0	0	0	0	0	1	0	0	0
A3	B1	0	0	1	1	0	0	0	0	0	0	0	0	1	0	0
A3	B2	0	0	1	0	1	0	0	0	0	0	0	0	0	1	0
A3	B3	0	0	1	0	0	1	0	0	0	0	0	0	0	0	1

		A			B			AB
A	B	1	2	3	1	2	3	11	12	13	21	22	23	31	32	33
A1	B1	1	0	0	1	0	0	1	0	0	0	0	0	0	0	0
A1	B2	1	0	0	0	1	0	0	1	0	0	0	0	0	0	0
A1	B3	1	0	0	0	0	1	0	0	1	0	0	0	0	0	0
A2	B1	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0
A2	B2	0	1	0	0	1	0	0	0	0	0	1	0	0	0	0
A2	B3	0	1	0	0	0	1	0	0	0	0	0	1	0	0	0
A3	B1	0	0	1	1	0	0	0	0	0	0	0	0	1	0	0
A3	B2	0	0	1	0	1	0	0	0	0	0	0	0	0	1	0
A3	B3	0	0	1	0	0	1	0	0	0	0	0	0	0	0	1