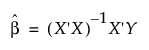Example of Analysis of Covariance with Unequal Slopes
Use the Standard Least Squares personality of the Fit Model platform to fit an analysis of covariance model. An analysis of covariance model is a model with a primary factor of interest and a covariate term. The covariate is a factor that is not the primary factor of interest, but could impact the effect of the primary factor on the response. In this example, drug is the primary factor of interest and x is the covariate.
Note: This analysis considers that the covariate impacts each level of the primary factor in a different manner. That is, a covariance model with unequal slopes. There is an interaction term included in the model. For an equal slopes model see Example of Analysis of Covariance with Equal Slopes.
1. Select Help > Sample Data Folder and open Drug.jmp.
2. Select Analyze > Fit Model.
3. Select y and click Y.
4. Select both Drug and x and click Macros > Factorial to Degree.
This adds terms up to the degree specified in the Degree box to the model. The default value for Degree is 2. Thus, the main effects of Drug and x, and their interaction, Drug*x, are added to the model effects list.
5. Click Run.
The coding used for Drug and the interaction between Drug and x is described in the Table 4.1.
|
Regressor |
Effect |
Values |
|
X1 |
Drug[a] |
+1 if a, 0 if d, –1 if f |
|
X2 |
Drug[d] |
0 if a, +1 if d, –1 if f |
|
X3 |
x |
the values of x |
|
X4 |
Drug[a]*(x - 10.733) |
x – 10.7333 if a, 0 if d, –(x – 10.7333) if f |
|
X5 |
Drug[d]*(x - 10.733) |
0 if a, x – 10.7333 if d, –(x – 10.7333) if f |
Report sections are shown and described below.
Regression Plot and Effect Tests
Use the Regression Plot to assess the model and to understand the impact of the covariate on the response. Use the Effects Tests for statistical tests of significance of the model effects.
Figure 4.23 Regression Plot and Effect Tests with Interaction
The Regression Plot shows that the response for Drug d and f increases at similar rates over the covariate, x. The response for Drug a tends to increase at a slower rate than for the other two drugs over the covariate, x. However, the Effect Test for the interaction has a p-value of 0.56. This is not significant, which indicates that the model does not need to include different slopes.
Perform a Spotlight Analysis
You now want to compare the least square means for the levels of Drug at a specific value of the covariate x. This type of comparison in an analysis of covariance model is sometimes referred to as spotlight analysis. For more information about spotlight analysis, see Spiller et al. (2013).
1. Select Multiple Comparisons from the Response y red triangle menu.
2. In the Multiple Comparisons window, select User-Defined Estimates.
3. Select all three values below Choose Drug Levels.
4. In the first box below x, enter 12.5.
5. Click Add Estimates.
This adds comparisons of the three levels of Drug at x = 12.5.
6. Click OK.
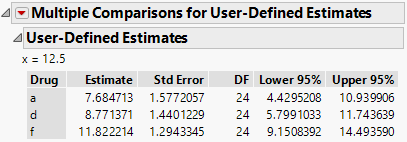
The User-Defined Estimates report shows least square means estimates for each level of Drug with the covariate x set to 12.5. The Multiple Comparisons for User-Defined Estimates red triangle menu contains options that enable you to test for differences among the estimates.
Figure 4.24 User-Defined Estimates Report
7. Select Comparisons with Overall Average. from the Multiple Comparisons for User-Defined Estimates red triangle menu.
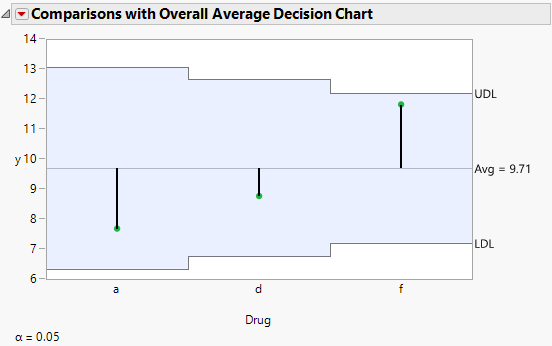
Figure 4.25 Comparisons with Overall Average Decision Chart
The Comparisons with Overall Average option shows an analysis of means (ANOM) chart for differences between the average and the three least squares means. From the ANOM chart, you conclude that there is not a significant effect of Drug on the response at x = 12.5.