Fit Distributions
Use the options in the Continuous Fit or Discrete Fit submenus to fit a distribution to a continuous variable. When you fit a distribution to a continuous variable, a curve is overlaid on the histogram and a Compare Distributions report and a Fitted Distribution report are added to the report window. A red triangle menu in the Fitted Distribution report contains additional options. See Fit Distribution Options. If a column contains a Distribution column property, the distribution in that column property is fit by default in the Distribution report.
Note: The Life Distribution platform also contains options for distribution fitting that might use different parameterizations and allow for censored observations. See Life Distribution in Reliability and Survival Methods.
Continuous Fit
The Continuous Fit submenu contains options for fitting continuous distributions. For more information about the parameterization of these distributions, see Statistical Details for Continuous Fit Distributions.
Fit Normal
Fits a normal distribution to the data. The normal distribution is often used to model symmetric data with most of the values falling in the middle of the curve. The parameter estimation for the normal distribution uses the unbiased estimate.
Fit Cauchy
Fits a Cauchy distribution to the data. The Cauchy distribution has an undefined mean and standard deviation. Although most data do not inherently follow a Cauchy distribution, it can be useful for estimating a robust location and scale for data that contain a large proportion of outliers (up to 50%).
Fit Student’s t
Fits a Student’s t distribution to the data. The Student’s t distribution is a robust option that spans the space between a normal distribution and a Cauchy distribution. As the degrees of freedom in the Student’s t distribution approach infinity, the distribution is equivalent to the normal. When the degrees of freedom in the Student’s t distribution equals 1, the distribution is equivalent to the Cauchy. The Distribution platform estimates the degrees of freedom value.
Fit SHASH
Fits a sinh-arcsinh (SHASH) distribution to the data. The SHASH distribution is similar to Johnson distributions in that it is a transformation to normality, but the SHASH distribution includes the normal distribution as a special case. This distribution can be symmetric or asymmetric.
Fit ZI SHASH
Fits a zero-inflated (ZI) sinh-arcsinh (SHASH) distribution to the data. The zero-inflated SHASH distribution is equivalent to a SHASH distribution with a point mass at zero. This distribution can be symmetric or asymmetric.
Fit Exponential
(Available only when all observations are nonnegative.) Fits an exponential distribution to the data. The exponential distribution is right-skewed and is often used to model lifetimes or the time between successive events.
Fit ExGaussian
Fits an exponentially modified Gaussian distribution to the data. The ExGaussian distribution is derived from adding a normal distribution and an exponential distribution. This distribution can be symmetric or asymmetric.
Fit Gamma
(Available only when all observations are positive.) Fits a gamma distribution to the data. The gamma distribution is a flexible distribution for modeling positive values.
Fit Lognormal
(Available only when all observations are positive.) Fits a lognormal distribution to the data. The lognormal distribution is right-skewed and is often used to model lifetimes or the time until an event. The parameter estimation for the lognormal distribution uses the maximum likelihood estimate.
Fit Weibull
(Available only when all observations are positive.) Fits a Weibull distribution to the data. The Weibull distribution is a flexible distribution and is often used to model lifetimes or the time until an event.
Fit Normal 2 Mixture
Fits a mixture of two normal distributions. This flexible distribution is capable of fitting bimodal data.
Fit Normal 3 Mixture
Fits a mixture of three normal distributions. This flexible distribution is capable of fitting multi-modal data.
Fit Smooth Curve
Fits a smooth curve using nonparametric density estimation. You can control the amount of smoothing by changing the kernel bandwidth using the slider that appears in the Nonparametric Density report. The kernel bandwidth is calculated as follows, where n is the number of unique observations and S is the uncorrected sample standard deviation:
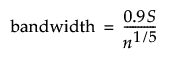
Fit Johnson
Fits a Johnson distribution to the data. The most appropriate of the three types of Johnson distribution (Su, Sb, and Sl) is fit and reported. The Johnson family of distributions is useful for its data-fitting capabilities because it supports every possible combination of skewness and kurtosis. Information about selection procedures and parameter estimation for the Johnson distributions can be found in Slifker and Shapiro (1980).
Fit Beta
(Available only when all observations are between 0 and 1.) Fits a beta distribution to the data. The beta distribution is useful for modeling data that are between 0 and 1 (not inclusive) and is often used to model proportions or rates.
Fit All
Fits all available continuous distributions to a variable. The Compare Distributions report contains statistics about each fitted distribution. By default, the best fit distribution is selected and displayed on the histogram. Use the check boxes to show or hide a fit report and overlay curve for the selected distribution. Initially, the Compare Distributions list is sorted by AICc in ascending order.
Tip: You can quickly remove distributions from the Compare Distributions list by double-clicking the name of the distribution in the Distribution column. This action also removes the corresponding Fitted Distribution report.
Enable Legacy Fitters
Shows or hides the Legacy Fitters submenu. Some features of distribution fitting were updated in JMP 15. This option enables you to use the older features from previous JMP releases that have been retained for compatibility purposes. For documentation on these legacy fitters, see the Details for the Legacy Distribution Fitters section of the JMP 16.1 Help.
Discrete Fit
The Discrete Fit submenu is available when all of the data values are integers. The Discrete Fit submenu contains options for fitting discrete distributions. For more information about the parameterization of these distributions, see Statistical Details for Discrete Fit Distributions.
Fit Poisson
Fits a Poisson distribution to the data. The Poisson distribution is useful for modeling the number of events in a given interval and is often expressed as count data.
Fit Negative Binomial
Fits a negative binomial distribution to the data. The negative binomial distribution is useful for modeling the number of successes before a specified number of failures. The negative binomial distribution is also equivalent to the Gamma Poisson distribution.
Fit ZI Poisson
(Available only when there are values of zero in the data.) Fits a zero-inflated Poisson distribution to the data. The zero-inflated Poisson distribution assumes a greater proportion of the data are zero values than would occur in a standard Poisson distribution.
Fit ZI Negative Binomial
(Available only when there are values of zero in the data.) Fits a zero-inflated negative binomial distribution to the data. The zero-inflated negative binomial distribution assumes a greater proportion of the data are zero values than would occur in a standard negative binomial distribution.
Fit Binomial
Fits a binomial distribution to the data. The binomial distribution is useful for modeling the total number of successes in n independent trials that all have a fixed probability, p, of success. The sample size can be specified as a fixed sample size for all observations, or it can be specified as another column in the data table that contains sample sizes for each row.
Note: When a non-constant sample size is specified, density curves, diagnostic plots, and profilers are not available.
Fit Beta Binomial
Fits a beta binomial distribution to the data. The beta binomial distribution is an overdispersed version of the binomial distribution. It requires a sample size greater than one for each observation. The sample size can be specified as a fixed sample size for all observations, or it can be specified as another column in the data table that contains sample sizes for each row.
Note: When a non-constant sample size is specified, density curves, diagnostic plots, and profilers are not available.
Fit ZI Binomial
(Available only when there are values of zero in the data.) Fits a zero-inflated binomial distribution to the data. The zero-inflated binomial distribution assumes a greater proportion of the data are zero values than would occur in a standard binomial distribution.
Note: When a non-constant sample size is specified, density curves, diagnostic plots, and profilers are not available.
Fit ZI Beta Binomial
(Available only when there are values of zero in the data.) Fits a zero-inflated beta binomial distribution to the data. The zero-inflated beta binomial distribution assumes a greater proportion of the data are zero values than would occur in a standard beta binomial distribution.
Note: When a non-constant sample size is specified, density curves, diagnostic plots, and profilers are not available.
Fit Distribution Options
Each fitted distribution report has a red triangle menu that contains additional options.
Density Curve
Uses the estimated parameters of the distribution to overlay a density curve on the histogram.
Diagnostic Plots
Contains options for diagnostic plots that enable you to visually check the goodness of fit for a fitted distribution. The plots are based on the idea that each sample data point estimates a quantile of the population. Contains the following options:
QQ Plot
Shows or hides a quantile-quantile (QQ) plot. This plot shows the relationship between the observations and the associated quantiles of the fitted distribution. A linear relationship shows evidence that the data follow the fitted distribution. QQ plots are also called probability plots.
Note: A Normal Quantile Plot is a QQ plot for a normal distribution. See Normal Quantile Plot for information about QQ plot construction.
PP Plot
Shows or hides a percentile-percentile (PP) plot. This plot shows the relationship between the empirical cumulative distribution function (CDF) and the fitted CDF.
Profilers
Contains the following options:
Distribution Profiler
Shows or hides a prediction profiler of the cumulative distribution function (CDF).
Quantile Profiler
Shows or hides a prediction profiler of the quantile function.
Save Columns
Contains the following options:
Save Density Formula
Saves a column to the data table that contains the density formula computed using the estimated parameter values.
Save Distribution Formula
Saves a column to the data table that contains the cumulative distribution function (CDF) formula computed using the estimated parameter values.
Save Simulation Formula
Saves a column to the data table that contains a formula that generates simulated values using the estimated parameters. This column can be used in the Simulate utility as a Column to Switch In. See Simulate.
Save Transformed
(Available only for Johnson and SHASH distribution fits.) Saves a column to the data table that contains a transform formula. The formula can be used to transform the analysis column to normality using the fitted distribution.
Goodness of Fit
(Not available for Johnson, Smooth Curve, or Normal Mixture distributions.) Shows or hides a Goodness-of-Fit Test report that contains a goodness-of-fit test for the fitted distribution.
For continuous fits, the goodness-of-fit test is the Anderson-Darling test. The p-value for the test is simulated using a parametric bootstrap, similar to the procedure described in Section 4.1 of Stephens (1974). For Normal distributions, the Shapiro-Wilk test for normality is also reported when the sample size is less than 2000 and there are no fixed parameters.
For discrete fits, the goodness-of-fit test is a Pearson chi-square test. For Binomial and Beta Binomial fits, the Goodness of Fit test is available only when the number of trials is constant.
Fix Parameters
(Not available for Johnson distribution or smooth curve fits.) Enables you to fix parameters and re-estimate the non-fixed parameters. An Adequacy LR (likelihood ratio) Test report also appears, which tests your new parameters to determine whether they fit the data.
Process Capability
(Not available for Cauchy, Student’s t, ZI SHASH, or discrete distribution fits.) Enables you to create a Process Capability analysis using the fitted distribution, which is a measure of how well process performs with respect to the specification limits. When you select the Process Capability option from a Fitted Distribution red triangle menu, a window appears with the following sections:
Enter Spec Limits
Enables you to manually enter specification limits. To use the fitted distribution to calculate specification limits, leave this section blank and use the options under Calculate Quantile Spec Limits Options.
Calculate Quantile Spec Limits Options
Enables you to calculate specification limits based on the fitted distribution. There are two methods available.
In the first method, you enter probabilities associated with the quantiles of the fitted distribution to calculate specification limits.
In the second method, you enter a K-Sigma Multiplier value that is used to calculate specification limits. This method has options for creating two-sided or one-sided limits.
After entering probabilities or a value for sigma multiplier, click Calculate Spec Limits to calculate the specification limits. These limits are entered into the Enter Spec Limits panel. Click OK to accept these limits and generate the Process Capability report. If the Use Calculated Spec Limits option is selected when you click OK, the specification limits that are used are based on the current probability or sigma multiplier values and you do not have to click the Calculate Spec Limits button. If the Save Spec Limits and Distribution to Column Properties without Report option is selected when you click OK, the corresponding column properties are saved to the data table and nothing is added to the Distribution report window.
Process Capability Options
Contains the following options:
The Moving Range Options outline contains options that enable you to select the type of moving range statistic. See Moving Range Options in Quality and Process Methods.
The Nonnormal Distribution Options outline contains options that enable you to select methods used for nonnormal process capability calculations. See Nonnormal Distribution Options in Quality and Process Methods.
For more information about the Process Capability options and report, see Process Capability in Quality and Process Methods.
Note: You can set preferences for many of the options in the Process Capability report in Distribution at File > Preferences > Platforms > Process Capability.
Remove Fit
Removes the distribution fit from the report window.