Mixed Models and Random Effect Models
A random effect model is a model where all of the factors represent random effects. See Random Effects. Such models are also called variance component models. Random effect models are often hierarchical models. A model that contains both fixed and random effects is called a mixed model. Repeated measures and split-plot models are special cases of mixed models. Often the term mixed model is used to subsume random effect models.
To fit a mixed model, you must specify the random effects in the Fit Model launch window. However, if all of your model effects are random, you can also fit your model in the Variability / Attribute Gauge Chart platform. Only certain models can be fit in this platform. Note that the fitting methods used in the Variability / Attribute Gauge Chart platform do not allow variance component estimates to be negative. For more information about how the Variability / Attribute Gauge Chart platform fits variance components models, see Variability Gauge Charts and Attribute Gauge Charts in Quality and Process Methods.
Random Effects
A random effect is a factor whose levels are considered a random sample from some population. Often, the precise levels of the random effect are not of interest, rather it is the variation reflected by the levels that is of interest (the variance components). However, there are also situations where you want to predict the response for a given level of the random effect. Technically, a random effect is considered to have a normal distribution with mean zero and nonzero variance.
Suppose that you are interested in whether two specific ovens differ in their effect on mold shrinkage. An oven can process only one batch of 50 molds at a time. You design a study where three randomly selected batches of 50 molds are consecutively placed in each of the two ovens. Once the batches are processed, shrinkage is measured for five parts randomly selected from each batch.
Note that Batch is a factor with six levels, one for each batch. So, in your model, you include two factors, Oven and Batch. Because you are specifically interested in comparing the effect of each oven on shrinkage, Oven is a fixed effect. But you are not interested in the effect of these specific six batches on the mean shrinkage. These batches are representative of a whole population of batches that could have been chosen for this experiment and to which the results of the analysis must generalize. Batch is considered a random effect. In this experiment, the Batch factor is of interest in terms of the variation in shrinkage among all possible batches. Your interest is in estimating the amount of variation in shrinkage that it explains. (Note that Batch is also nested within Oven, because only one batch can be processed once in one oven.)
Now suppose that you are interested in the weight of eggs for hens subjected to two feed regimes. Ten hens are randomly assigned to feed regimes: Five are given Feed regime A and five are given Feed regime B. However, these ten hens have some genetic differences that are not accounted for in the design of the study. In this case, you are interested the predicted weight of the eggs from certain specific hens as well as in the variance of the weights of eggs among hens.
The Classical Linear Mixed Model
JMP fits the classical linear mixed effects model:
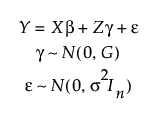
Here,
• Y is an n x 1 vector of responses
• X is the n x p design matrix for the fixed effects
• β is a p x 1 vector of unknown fixed effects with design matrix X
• Z is the n x s design matrix for the random effects
• γ is an s x 1 vector of unknown random effects with design matrix Z
• ε is an n x 1 vector of unknown random errors
• G is an s x s diagonal matrix with identical entries for each level of a categorical random effect and a single entry for each continuous random effect
• In is an n x n identity matrix
• γ and ε are independent
The diagonal elements of G, as well as σ2, are called variance components. These variance components, together with the vector of fixed effects β and the vector of random effects γ, are the model parameters that must be estimated.
The covariance structure for this model is sometimes called the variance component structure (SAS Institute Inc. 2023d). This covariance structure is the only one available in the Standard Least Squares personality.
 The Mixed Model personality fits a variety of covariance structures, including Residual, First-order Autoregressive (or AR(1)), Unstructured, and Spatial. See Repeated Structure Tab.
The Mixed Model personality fits a variety of covariance structures, including Residual, First-order Autoregressive (or AR(1)), Unstructured, and Spatial. See Repeated Structure Tab.
REML versus EMS for Fitting Models with Random Effects
JMP provides two methods for fitting models with random effects:
• REML, which stands for restricted maximum likelihood (always the recommended method)
• EMS, which stands for expected mean squares (use only for teaching from old textbooks)
The REML method is now the mainstream fitting methodology, replacing the traditional EMS method. REML is considerably more general in terms of applicability than the EMS method. The REML approach was pioneered by Patterson and Thompson (1974). See also Wolfinger et al. (1994) and Searle et al. (1992).
The EMS method, also called the method of moments, was developed before the availability of powerful computers. Researchers restricted themselves to balanced situations and used the EMS methodology, which provided computational shortcuts to compute estimates for random effect and mixed models. Because many textbooks still in use today use the EMS method to introduce models containing random effects, JMP provides an option for EMS. (See, for example, McCulloch et al., 2008; Poduri, 1997; Searle et al., 1992.)
The REML methodology performs maximum likelihood estimation of a restricted likelihood function that does not depend on the fixed-effect parameters. This yields estimates of the variance components that are then used to obtain estimates of the fixed effects. Estimates of precision are based on estimates of the covariance matrix for the parameters. Even when the data are unbalanced, REML provides useful estimates, tests, and confidence intervals.
The EMS methodology solves for estimates of the variance components by equating observed mean squares to expected mean squares. For balanced designs, a complex set of rules specifies how estimates are obtained. There are problems in applying this technique to unbalanced data.
For balanced data, REML estimates are identical to EMS estimates. But, unlike EMS, REML performs well with unbalanced data.
Specifying Random Effects and Fitting Method
Models with random effects are specified in the Fit Model launch window. To specify a random effect, highlight it in the Construct Model Effects list and select Attributes > Random Effect. This appends &Random to the effect name in the model effect list. For a definition of random effects, see Random Effects. Random effects can also be specified in a separate effects tab. See Construct Model Effects Tabs.
In the Fit Model launch window, once the &Random attribute has been appended to an effect, you are given a choice of fitting Method: REML (Recommended) or EMS (Traditional).
Caution: You must declare crossed and nested relationships explicitly. For example, a subject ID might also identify the group that contains the subject, as when each subject is in only one group. In such a situation, subject ID must still be declared as nested within group. Take care to be explicit in defining the design structure.
Unrestricted Parameterization for Variance Components
There are two different approaches to parameterizing the variance components: the unrestricted and the restricted approaches. The issue arises when there are mixed effects in the model, such as the interaction of a fixed effect with a random effect. Such an interaction term is considered to be a random effect.
In the restricted approach, for each level of the random effect, the sum of the interaction effects across the levels of the fixed effect is assumed to be zero. In the unrestricted approach, the mixed terms are simply assumed to be independent random realizations of a normal distribution with mean 0 and common variance. (This assumption is analogous to the assumption typically applied to residual error.)
JMP and SAS use the unrestricted approach. This distinction is important because many statistics textbooks use the restricted approach. Both approaches have been widely taught for 60 years. For a discussion of both approaches, see Cobb (1998, Section 13.3).
Negative Variances
Though variances are always positive, it is possible to have a situation where the unbiased estimate of the variance is negative. Negative estimates can occur in experiments when an effect is very weak or when there are very few levels corresponding to a variance component. By chance, the observed data can result in an estimate that is negative.
Unbounded Variance Components
JMP can produce negative estimates for both REML and EMS. For REML, there are two options in the Fit Model launch window: Unbounded Variance Components and Estimate Only Variance Components. The Unbounded Variance Components option is selected by default. Deselecting this option constrains variance component estimates to be nonnegative.
You should leave the Unbounded Variance Components option selected if you are interested in fixed effects. Constraining the variance estimates to be nonnegative leads to bias in the tests for the fixed effects.
Estimate Only Variance Components
Select this option if you want to see only the REML Variance Component Estimates report. If you are interested only in variance components, you might want to constrain variance components to be nonnegative. Deselecting the Unbounded Variance Components option and selecting the Estimate Only Variance Components option might be appropriate.