Space-Filling Designs
Space-filling designs are useful in situations where run-to-run variability is of far less concern than the form of the model. Space filling designs include sphere packing Latin hypercube, uniform, minimum potential, maximum entropy, Gaussian process, and fast flexible designs.
Consider a sensitivity study of a computer simulation model. In this situation, and for any mechanistic or deterministic modeling problem, any variability is small enough to be ignored. For systems with no variability, replication, randomization, and blocking are irrelevant.
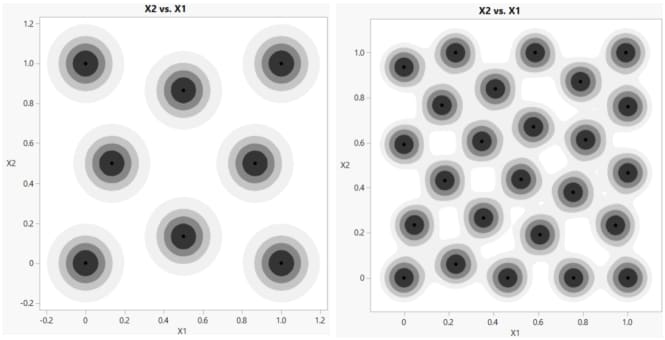
The Space Filling platform provides multiple design types for situations with only continuous factors. A special design type exists for designs that include categorical, discrete numeric or mixture factors. For continuous factors, space-filling designs have two objectives:
• maximize the distance between any two design points
• space the points uniformly
Figure 21.1 Space-Filling Design