Statistical Details for Assess Variable Importance
This section contains details that relate to the how the variable importance indices in the Prediction Profiler are calculated.
Background
Denote the function that represents the predictive model by f, and suppose that x1, x2, ..., xn are the factors, or main effects, in the model. Let y = f(x1, x2 ..., xn).
• The expected value of y, E(y), is defined by integrating y with respect to the joint distribution of x1, x2, ..., xn.
• The variance of y, Var(y), is defined by integrating (y – E(y))2 with respect to the joint distribution of x1, x2, ..., xn.
Main Effect
The impact of the main effect xj on y can be described by Var(E(y |xj)). Here the expectation is taken with respect to the conditional distribution of x1, x2, ..., xn given xj, and the variance is taken over the distribution of xj. In other words, Var(E(y |xj)) measures the variation, over the distribution of xj, in the mean of y when xj is fixed.
It follows that the ratio Var(E(y |xj))/Var(y) gives a measure of the sensitivity of y to the factor xj. The importance index in the Main Effect column in the Summary Report is an estimate of this ratio. (See Adjustment for Sampling Variation.)
Total Effect
The Total Effect column represents the total contribution to the variance of y = f(x1, x2 ..., xn) from all terms that involve xj. The calculation of Total Effect depends on the concept of functional decomposition. The function f is decomposed into the sum of a constant and functions that represent the effects of single variables, pairs of variables, and so on. These component functions are analogous to main effects, interaction effects, and higher-order effects. See Saltelli (2002); Sobol (1993).
Those component functions that include terms containing xj are identified. For each of these, the variance of the conditional expected value is computed. These variances are summed. The sum represents the total contribution to Var(y) due to terms that contain xj. For each xj, this sum is estimated using the selected methodology for generating inputs. The importance indices reported in the Total Effect column are these estimates. (See Adjustment for Sampling Variation.)
Consider a simple example with two factors, x1 and x2. Then the Total Effect importance index for x1 is an estimate of the following:
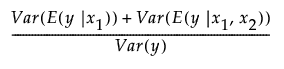
Adjustment for Sampling Variation
Due to the fact that they are obtained using sampling methods, the Main Effect and Total Effect estimates shown in the Summary Table might have been adjusted. Specifically, if the Total Effect estimate is less than the Main Effect estimate, then the Total Effect importance index is set equal to the Main Effect estimate. If the sum of the Main Effect estimates exceeds one, then these estimates are normalized to sum to one.
Variable Importance Standard Errors
The standard errors that are provided for independent inputs measure the accuracy of the Monte Carlo replications. Importance indices are computed as follows:
• Latin hypercube sampling is used to generate a set of data values.
• For each set of data values, main and total effect importance estimates are calculated.
• This process is replicated until the estimated standard errors of the Main Effect and Total Effect importance indices for all factors fall below a threshold of 0.01.
The standard errors that are reported are the standard error values in effect when the replications terminate.