Utiliser la régression avec un régresseur
Si vous avez une variable Y continue et une variable X continue unique, vous pouvez créer un modèle de régression simple.
Scénario
Cet exemple s'appuie sur la table de données Companies.jmp, qui contient des données financières sur 32 sociétés des industries pharmaceutique et informatique.
Il est tentant de penser que les sociétés avec un grand nombre d’employés génèrent un plus gros chiffre d'affaires que les sociétés à effectif réduit. Un analyste souhaite prévoir le chiffre d'affaires de chaque société en se basant sur le nombre d’employés.
Pour exécuter cette tâche, procédez comme suit :
• Ajuster le modèle de régression
Découvrir la relation
Tout d’abord, créez un nuage de points pour visualiser la relation entre le nombre d’employés et le chiffre d'affaires. Ce nuage de points a été créé au paragraphe Créer le nuage de points. La Figure 5.12 illustre les résultats obtenus après masquage et exclusion d'une valeur aberrante (une société avec un effectif et un chiffre d'affaires très importants).
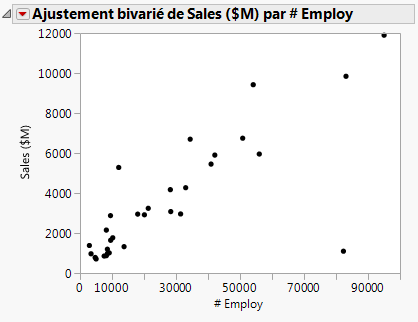
Figure 5.12 Nuage de points de Sales ($M) par rapport à # Employ
Ce nuage de points donne une image plus claire de la relation entre les ventes et le nombre d’employés. Comme on pouvait s’y attendre, plus une société a d’employés, plus elle génère de chiffre d'affaires. Cela confirme visuellement l'hypothèse de l’analyste, sans donner d'indication précise sur le chiffre d'affaires pour un nombre donné d'employés.
Ajuster le modèle de régression
Pour prévoir un chiffre d'affaires d'après un nombre d’employés, vous devez ajuster un modèle de régression. Cliquez sur le triangle rouge Ajustement bivarié et sélectionnez Régression simple. Une droite de régression est ajoutée dans le nuage de points et des rapports sont ajoutés dans la fenêtre de rapport.
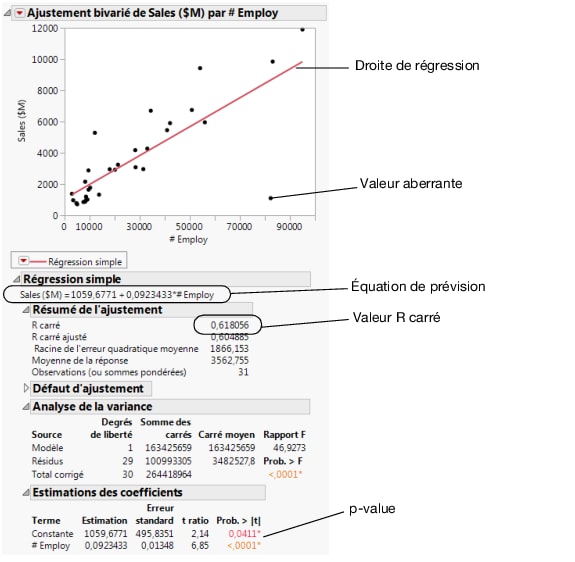
Figure 5.13 Droite de régression
Dans les rapports, observez les résultats suivants :
• la p-value <0.0001
• La valeur R carré de 0,618
D’après ces résultats, l’analyste peut tirer les conclusions suivantes :
• La p-value du terme du modèle #Employ est petite. Cela permet d'établir qu'au niveau de significativité de 0,05 le coefficient est différent de zéro pour #Employ. Par conséquent, en incluant le nombre d’employés dans le modèle de prévision, il est possible d'augmenter de façon significative la capacité de prévision du chiffre d'affaires moyen en comparaison avec un modèle n'incluant pas le nombre d'employés.
• La valeur R carré de 0,618 indique que ce modèle explique environ 62 % de la variabilité du chiffre d'affaires. La valeur R carré est le coefficient de détermination et indique la proportion la variance dans la variable dépendante (réponse) qui est expliquée par votre modèle. R carré est compris entre 0 et 1. Un modèle avec un R carré de 0 n'a pas de pouvoir explicatif. Un modèle avec un R carré de 1 prévoit parfaitement la réponse.
Prévoir les ventes moyennes
Utilisez le modèle de régression pour prévoir le chiffre d'affaires moyen d'une société en fonction de son nombre d’employés. L’équation de prévision du modèle est incluse dans le rapport :
Chiffre d'affaires moyen = 1059,68 + 0,092*employés
Par exemple, dans une entreprise comptant 70 000 employés, il est prévu que le chiffre d'affaires soit d'environ 7 500 $ :
7 499,68 $ = 1 059,68 + 0,092*70 000
En bas à droite du nuage de points, une valeur aberrante ne suit pas le modèle général des autres sociétés. L’analyste aimerait savoir si le modèle de prévision change lorsque cette valeur aberrante est exclue.
Exclure la valeur aberrante
1. Cliquez sur la valeur aberrante.
2. Choisissez Lignes > Exclure/Annuler l’exclusion.
3. Pour ajuster ce modèle, cliquez sur le triangle rouge en regard d'Ajustement bivarié de Sales ($M) par # Employ et sélectionnez Régression simple.
Voici ce qui est ajouté dans la fenêtre de rapport (Figure 5.14) :
• Une nouvelle droite de régression
• Un nouveau rapport Régression simple comprenant :
– Une nouvelle équation de prévision
– Une nouvelle valeur R carré
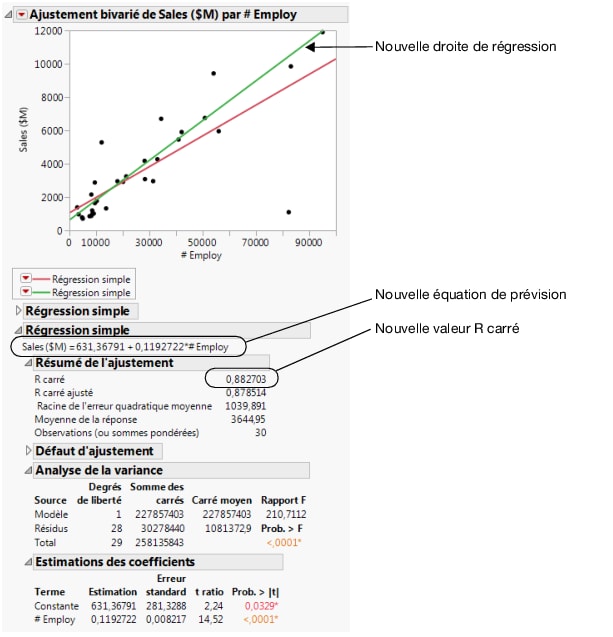
Figure 5.14 Comparer les modèles
Interpréter les résultats
Les résultats de la Figure 5.14 permettent à l’analyste de tirer les conclusions suivantes :
• La valeur aberrante faisait baisser la droite de régression des plus grandes sociétés et faisait monter la droite des plus petites.
• Le nouveau modèle, excluant la valeur aberrante, est plus fiable que le précédent. La nouvelle valeur R carré de 0,88 est plus élevée et plus proche de 1.
Tirer les conclusions
La nouvelle équation de prévision permet de calculer le chiffre d'affaires prévisionnel moyen d’une société de 70 000 employés comme suit :
8 961,37 $ = 631,37 + 0,119*70 000
La prévision établie à partir du premier modèle était d'environ 7 500 $. Le second modèle prévoit un chiffre d'affaires total d'environ 8 960 $, soit 1 460 $ de plus qu'avec le premier modèle.
Par rapport au premier modèle et après suppression de la valeur aberrante, le second modèle décrit et prévoit mieux le chiffre d'affaires total en fonction du nombre d’employés. L’analyste dispose désormais d'un modèle efficace.