［多重比較］オプションを用いると、ある群と別の群との平均を比較し、その差の信頼区間を求めることができます。多重比較法の目的は、全体において第1種の誤りを犯す確率が大きくなるので、多重性を調整することです。［多重比較］オプションでは、全体平均との比較（ANOM型の比較）や、コントロール群との比較（Dunnett型の比較）が行えます。また、すべてのペアを比較する検定として、TukeyのHSD検定とStudentのt検定が行えます。Studentのt検定においては同等性検定も行えます。同等性検定では、実質的にゼロとみなす差を指定する必要があります。
Studentのt検定は、1つ1つの比較の第1種の誤りしか制御しません。そのため、Studentのt検定は、「多重比較」の手法とは言えないでしょう。Studentのt検定以外の手法は、比較全体における第1種の誤りを制御します。言い換えると、Studentのt検定以外の手法は、p値や信頼区間の計算において、多重性を調整しています。
［最小2乗平均の推定値］の起動ウィンドウは、［多重比較］オプションの設定パネルです。この例では、「Big Class.jmp」サンプルデータにて、「体重(ポンド)」を応答変数、「年齢」、「性別」、および「身長(インチ)」をモデル効果に指定しています。設定パネルでは、［最小2乗平均の推定値］と［ユーザ定義の推定値］という2種類のいずれかで、比較を指定できます。
このオプションは最小2乗平均を比較するもので、名義尺度または順序尺度の効果に対してだけ使えます。最小2乗平均は、他の効果を中立的な値に固定した時の応答の予測値です （最小2乗平均の定義については、第 “最小2乗平均表”を参照）。この比較を行うには、比較を行いたい効果を選択してください。［最小2乗平均の推定値］の起動ウィンドウでは、「年齢」の［最小2乗平均の推定値］が指定されています。最小2乗平均プロットを表示するオプションがあります。第 “最小2乗平均プロットのオプション”を参照してください。
図3.28 ［最小2乗平均の推定値］の起動ウィンドウ
［ユーザ定義の推定値］の起動ウィンドウは、［ユーザ定義の推定値］の設定を示しています。年齢の3水準と性別の2水準を選択しています。また、身長の2つの値をキーボードで入力しています。その後、［推定値の追加］ボタンをクリックすると、図のように、指定された水準を組み合わせたリストが表示されます。なお、この状態で、さらに推定値を指定し、［推定値の追加］ボタンを再度クリックし、「比較の推定値」リストにそれらを追加することもできます。
図3.29 ［ユーザ定義の推定値］の起動ウィンドウ
［最小2乗平均プロットの表示］オプションを選択すると、最小2乗平均プロットが描かれます。このオプションを選択した場合で、選択している効果が交互作用項である時には、交互作用プロットの作成に関するオプションのパネルが表示されます。このパネルで、重ね合わせる項を選択してください。交互作用プロットを選択しなかった場合には、すべての因子の水準を組み合わせた最小2乗プロットが描かれます。第 “最小2乗平均プロットのオプション”を参照してください。
有意性検定のt値。この列は、レポートを右クリックし、［列］>［t値］を選択した場合のみ表示されます。
有意性検定のp値。この列は、レポートを右クリックし、［列］>［p値(Prob>|t|)］を選択した場合のみ表示されます。
このオプションは、各グループの平均を、全体平均と比較します。また、全体平均との差の信頼区間を、表とグラフで示します。この手法は、平均分析（ANOM; analysis of means）と呼ばれます（Nelson, et al., 2005）。この比較では、各グループの平均を全体平均と比較するので、複数回の比較が行われます。平均分析では、複数回の比較で生じる多重性を調整しています。レーティングの全体平均との比較は、「Lipid Data.jmp」サンプルデータの例です。
この重み付き平均の重みには、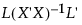
の対角要素の逆数が使われます。ここで、Lは、最小2乗平均を算出する係数からなる行列です。最小2乗平均については、『SAS/STAT 14.3 User’s Guide』（SAS Institute Inc. 2017）の「GLM Procedure」章を参照してください。
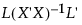の対角要素の逆数が使われます。ここで、Lは、最小2乗平均を算出する係数からなる行列です。最小2乗平均については、『SAS/STAT 14.3 User’s Guide』（SAS Institute Inc. 2017）の「GLM Procedure」章を参照してください。ユーザ定義の推定値でも、平均分析での全体平均は、同様に推定値の重み付き平均として定義されます。この場合、Lは推定値を算出する係数からなる行列になります。
|
–
|
Nelson法: この方法は、正確な棄却値とp値を算出します。Nelson法は、推定値の間に相関がない場合だけに使えます。
|
|
–
|
技術的な詳細については、『SAS/STAT 14.3 User’s Guide』（SAS Institute Inc. 2017）の「GLM Procedure」章を参照してください。
|
•
|
p値（Prob>|t|）を含む列を「全体平均との比較」レポートに追加します。バランスが取れていないデータや複雑な比較などでは積分が複雑になり、Nelson法やNelson-Hsu法で棄却値やp値を求められないときがあります。そのような場合は、Sidak法によって棄却値が計算されます（このとき、p値は計算されません）。
「Lipid Data.jmp」サンプルデータを例に見てみましょう。飲酒状況と心疾患既往歴を制御しながら、「喫煙歴」の4群のいずれかで、1日あたりの「コーヒーの摂取量」がその全体平均と異なっているかどうかを調べてみます。「コーヒーの摂取量 (カップ/日)」を応答とし、「喫煙歴」、「飲酒状況」および「心臓病歴」をモデル効果として指定します。
|
1.
|
［ヘルプ］>［サンプルデータライブラリ］を選択し、「Lipid Data.jmp」を開きます。
|
|
2.
|
［分析］>［モデルのあてはめ］を選択します。
|
|
3.
|
「コーヒーの摂取量 (カップ/日)」を選択し、Yをクリックします。
|
|
4.
|
|
5.
|
［実行］をクリックします。
|
|
6.
|
「応答 コーヒーの摂取量 (カップ/日)」の横の赤い三角ボタンのメニューから、［推定値］>［多重比較］を選択します。
|
|
7.
|
「効果の選択」リストから、［喫煙歴］を選択します。
|
|
8.
|
「比較の選択」リストから、［全体平均との比較 - ANOM］を選択します。
|
|
9.
|
［OK］をクリックします。
|
レーティングの全体平均との比較の結果からわかるように、非喫煙者とたばこ喫煙者の最小2乗平均は、コーヒー摂取に関して全体平均とは有意に異なっています。
図3.30 レーティングの全体平均との比較
コントロール群を選択し、［OK］をクリックすると、「最小2乗法によるあてはめ」レポートに「コントロール群との比較」レポートが表示されます。このオプションは、指定された水準の平均をコントロール群の平均と比較します。また、コントロール群との差の信頼区間に関する表と、決定限界に関するグラフを作成します。p値や信頼区間の計算には、Dunnett法が使われます。Dunnett法は、コントロール群との比較の全体において、第1種の誤りを犯す確率を制御します（Hsu, 1996 and Westfall et al., 2011）があります。
Dunnett法での正確な計算ができない状況では、Hsuの因子分析型近似法が使われます（Hsu, 1992）。バランスが取れていないデータや複雑な比較などでは積分が複雑になり、棄却値やp値を求められないときがあります。そのような場合は、Sidak法によって棄却値が計算されます。
|
–
|
Dunnett法: この方法は、正確な棄却値とp値を算出します。Dunett法は、推定値の間に相関がない場合だけに使えます。
|
|
–
|
技術的な詳細については、『SAS/STAT 14.3 User’s Guide』（SAS Institute Inc. 2017）の「GLM Procedure」章を参照してください。
|
•
|
p値（Prob>|t|）を含む列を「コントロール群との比較」レポートに追加します。バランスが取れていないデータや複雑な比較などでは積分が複雑になり、Dunnett法やDunnett-Hsu法で棄却値やp値を求められないときがあります。そのような場合は、Sidak法によって棄却値が計算されます（このとき、p値は計算されません）。
すべてのペアを比較する検定として、「すべてのペアの比較 ‐ TukeyのHSD検定」と「各ペアの比較 ‐ Studentのt検定（Hsu 1996; Westfall et al.」 2011）があります。TukeyのHSD検定は、すべてのペアの比較に関して有意水準が保たれています（Hsu, 1996およびWestfall et al., 2011）。一方、Studentのt検定は、1つ1つの比較のみにしか有意水準が保たれていません。Studentのt検定を用いた場合、行った複数の比較のうちのいずれか1つで第1種の誤りを犯す確率は、設定した有意水準をかなり超えてしまいます。
検定の棄却値。TukeyのHSD検定では、分位点は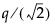
です。ここで、qはスチューデント化された範囲の分位点です。
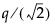です。ここで、qはスチューデント化された範囲の分位点です。|
–
|
Tukey法: この方法は、正確な棄却値とp値を算出します。この方法は、推定値の間に相関がなく、かつ、推定値の分散が等しい場合にだけ使えます。バランスが取れているデータ（釣合い型データ）の場合には、この条件を満たしています。
|
|
–
|
Tukey-Kramer法: この方法は、棄却値とp値の近似値を算出します。Tukey法が使えないような状況で使用されます。
|
技術的な詳細については、『SAS/STAT 14.3 User’s Guide』（SAS Institute Inc. 2017）の「GLM Procedure」章を参照してください。
TukeyのHSD検定も、Studentのt検定も、水準のすべてのペアを比較します。それぞれのペアに対して、レポートには次の統計量が表示されます。
|
•
|
「ペア比較の散布図」は、すべてのペアについて、平均差の信頼区間を描いたグラフです。ディフォグラム（diffogram）や、平均-平均散布図（mean-mean scatterplot）などとも呼ばれています。ユーザ定義の推定値のペア比較の散布図に、このグラフの例を示しています。有意な差が分かるように、色分けされています。
このオプションを選択すると、同等性検定が行われます。実質的に意味がある差の範囲内にあることを検証したい場合には、同等性検定が役立ちます。この検定においては、特定の閾値を指定し、その閾値内に母平均の差が収まっている場合には「母平均は実質的に等しい」と見なします。つまり、2つのグループの母平均の差が閾値以下である場合は、それらは同等であると見なします。
ダイアログで閾値を設定して分析を実行すると、「同等性検定」レポートが表示されます。指定した閾値は、レポートの上部に表示されます。レポートは、同等性検定の表とグラフで構成されます。同等性検定と信頼区間は、Studentのt分布に基づいて計算されています
同等性検定には、2回の片側検定法（TOST metod; Two One-Sided Tests metod）を用いています（Schuirmann, 1987）。この方法では、「真の差は、閾値を超えている」という帰無仮説を検定するために、プールした分散に基づく片側t検定を2回、行います。2回の検定が両方ともこの帰無仮説を棄却すれば、「母平均の差は、上限値と下限値のどちらの閾値も超えていない」とみなされます。したがって、母平均の差は実質的に等しいとみなされます。どちらか一方だけ棄却されたか、または、どちらの検定も棄却されなかった場合は、統計的に有意ではありません。
|
•
|
|
•
|
最大p値 - 2つの片側t検定のp値のうち大きいほうの値
|
信頼区間の下限および上限
信頼区間を表しています。線分上の中点の座標は、差の点推定値を表しています。これらの点をクリックすると、グループ名と差の推定値を示すツールヒントが呼び出されます。対角線上の帯の中に完全に線分が含まれている場合、平均が実質的に同等であることを示しています。「Lipid Data.jmp」サンプルデータを例に見てみましょう。性別（男性と女性）、年齢（25歳と35歳）、喫煙状況（非喫煙者と元喫煙者。それぞれ「喫煙歴」が「no」と「quit」）の組み合わせで構成される群について、平均身長における「コレステロール」の違いを調べてみます。
|
1.
|
［ヘルプ］>［サンプルデータライブラリ］を選択し、「Lipid Data.jmp」を開きます。
|
|
2.
|
［分析］>［モデルのあてはめ］を選択します。
|
|
3.
|
「コレステロール」を選択し、［Y］をクリックします。
|
|
4.
|
|
5.
|
［実行］をクリックします。
|
|
6.
|
「応答 コレステロール」の横の赤い三角ボタンのメニューから、［推定値］>［多重比較］を選択します。
|
|
7.
|
「推定値の種類」リストから［ユーザ定義の推定値］をクリックします。
|
|
8.
|
|
9.
|
|
10.
|
［年齢］リストで、最初の2つの行にぞれぞれ「25」、「35」を入力します。
|
|
11.
|
［推定値の追加］をクリックします。
|
|
12.
|
「比較の選択」リストで、［すべてのペアの比較 - TukeyのHSD検定］を選択します。
|
これで、ウィンドウがユーザ定義の推定値を指定のようになっていることを確認します。
図3.31 ユーザ定義の推定値を指定
|
13.
|
［OK］をクリックします。
|
「すべてのペアの平均差」レポートを見ると、28個のペアの比較の中で2つが有意になっています。「ペア比較の散布図」（ユーザ定義の推定値のペア比較の散布図）では、これらの比較の信頼区間が赤色になっています。いずれかの点の上にポインタを置いて、その点がどのペアの比較を表しているかを決定することができます。ツールヒントには、比較の2つの水準の間の差も含まれています。ユーザ定義の推定値のペア比較の散布図の2つの赤い点は、35歳の元喫煙者と25歳の非喫煙者を男女について比較している点を表しています。
図3.32 ユーザ定義の推定値のペア比較の散布図
