［一般化線形混合モデル］手法の別例
この例では、「モデルのあてはめ」プラットフォームで［一般化線形混合モデル］手法を使って、製造工程を分析します。データテーブルには、ロット、ロット内のユニット、各ユニットに施された仕上げ処理の回数が含まれます。ロットおよびロット内ユニットは無作為抽出されています。ユニットごとに不適合数を数え、この数を10未満に抑えられるような仕上げ処理の水準を特定したいとしましょう。この計画は、乱塊法（完備型ブロック計画）に基づいています。なお、応答変数（不適合数）は正規分布に従いません。
1. ［ヘルプ］>［サンプルデータフォルダ］を選択し、「Manufacturing Defect Counts.jmp」を開きます。
2. ［分析］>［モデルのあてはめ］を選択します。
3. 「不適合数」を選択し、［Y］をクリックします。
この列を［Y］として追加すると、「手法」が［標準最小2乗］になります。
4. 「手法」リストから［一般化線形混合モデル］を選択します。または、［一般化線形混合モデル］手法を選択してから、［Y］をクリックして「不適合数」を追加することもできます。
5. 「分布」リストから［Poisson］を選択します。
6. 「最終処理」を選択し、［固定効果］タブの［追加］をクリックします。
図9.9 指定が完了した「モデルのあてはめ」起動ウィンドウの［変量効果］タブ
7. ［変量効果］タブをクリックします。
8. 「ロット」を選択し、［追加］をクリックします。
9. 「列の選択」リストから「最終処理」を選択し、［変量効果］タブで「Lot」を選択して、［交差］をクリックします。
図9.10 入力が完了した「モデルのあてはめ」起動ウィンドウ、［変量効果］タブ
10. ［実行］をクリックします。
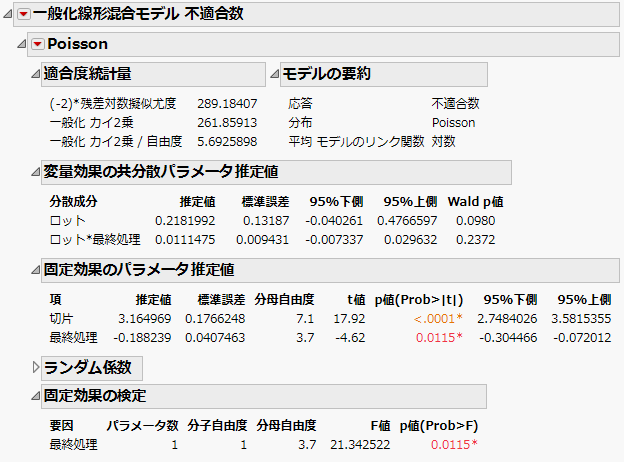
図9.11 「一般化線形混合モデル」レポートウィンドウ
「一般化線形混合モデル」レポートの「適合度統計量」セクションで、「一般化 カイ2乗 / 自由度」が5.69であることに注目してください。この値は1よりはるかに大きいので、モデルと比較して、データに過分散があることが示唆されています。次に、項をさらに追加したモデルにあてはめて、過分散の原因を調べてみましょう。
11. 「一般化線形混合モデル 不適合数」の赤い三角ボタンをクリックし、［モデルダイアログ］を選択します。
このオプションを選択すると、「モデルのあてはめ」起動ウィンドウが開き、先ほどの選択内容が再現されます。
12. ［変量効果］タブをクリックします。
13. 「列の選択」リストから「ロット内ユニット」を選択し、［変量効果］タブで「ロット」を選択して、［交差］をクリックします。
図9.12 入力が完了した「モデルのあてはめ」起動ウィンドウ、［変量効果］タブ
14. ［実行］をクリックします。
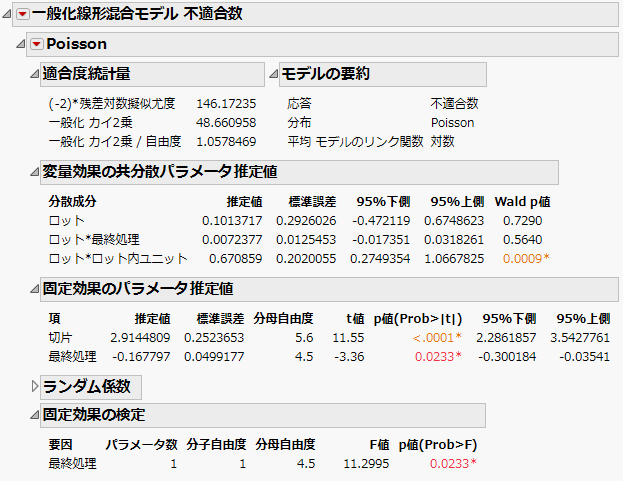
図9.13 「一般化線形混合モデル」レポートウィンドウ
「一般化線形混合モデル」レポートの「適合度統計量」セクションで、「一般化 カイ2乗 / 自由度」が1.06になったことに注目してください。この値は1に近いため、データの過分散が説明されたことが示されています。次に、このモデルを使って、不適合数を10未満におさえるような仕上げ処理の水準を特定します。
15. 「Poisson」の赤い三角ボタンをクリックし、［周辺予測値プロット］>［プロファイル］を選択します。
「周辺モデルプロファイル」には、ロットの効果が0である場合の推論が示されるので、将来のロットについて推論するのに役立ちます。
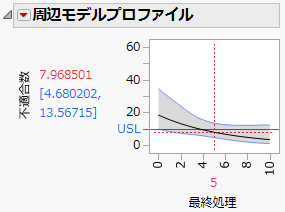
図9.14 不適合の数に対する周辺モデルプロファイル
このプロファイルによると、仕上げ処理の水準が5の場合の不適合数の予測値は約8個ですが、予測値の95%信頼区間には10個が含まれています。仕上げ処理の水準を10に上げても、不適合数の予測値の信頼区間には10個が含まれています。この実験における仕上げ処理の水準の最大値は10なので、外挿を避けるため、仕上げ処理の水準をもっと大きく設定して追加実験を行うことが推奨されます。