正準プロットと正準構造
「判別分析」レポートの正準プロットは変数の正準相関構造を示すバイプロットです。
正準構造
正準プロットでは、[X, カテゴリ]列から作成されるダミー変数(指示変数)の線形結合と、共変量の線形結合との相関が最大になるようなスコアが求められます。そうやって求められた共変量の線形結合(正準スコア)がプロットされます。このようにして求められた正準スコアは、グループ間の距離が最大となっています。
第1次元の正準スコアは、グループ(カテゴリ)から作成されたダミー変数の線形結合と、共変量の線形結合との相関が最大化となるときの、共変量の線形結合です。第2次元では、第1次元の正準スコアと直交するという条件のもとで、やはり相関が最大になるような線形結合が求められます。[X, カテゴリ]の列における水準がk個の場合は、k - 1次元の正準スコアが求められます。
正準プロット
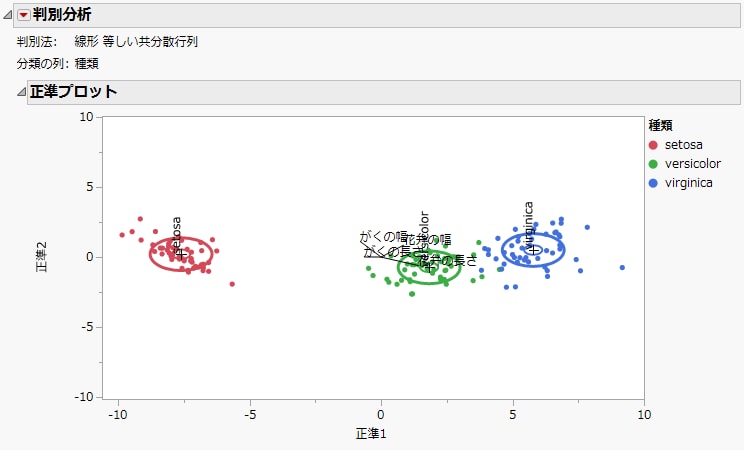
Figure 5.7は、「Iris.jmp」の線形判別分析の「正準プロット」を示しています。点は、「種類」によって色分けされています。
図5.7 「Iris.jmp」の正準プロット
バイプロットの横軸と縦軸は、最初の2つの正準変数です。これらの正準変数は、グループ間の距離が最大となる2次元です。各正準変数はそれぞれ共変量の線形結合です(正準構造を参照)。このバイプロットを見ると、各データ行がどのように分布しているかや、各共変量が正準変数にどのように寄与しているかがわかります。
• バイプロットでは、各グループの多変量平均と各データ行が点で示されます。これらが、最初の2つの正準変数に表現されています。
– 各多変量平均に対応する点は、プラス記号(+)のマーカーで示されます。
– 各平均の95%信頼楕円がプロットされます。かなり大雑把に言うと、2つのグループの平均が有意に異なる場合、信頼楕円は交わらず、離れている傾向にあります。
– 各グループの50%確率楕円も描かれます。この楕円は、正規分布に従うと仮定したときの(かつ、線形判別分析では、等しい共分散行列に従うと仮定したときの)、データ点のおよそ50%を含む領域を表しています。
• バイプロット上に描かれているバイプロット線は、共変量を表しています。
– 共変量の線形結合(正準変数)の係数は、正準空間を構成するための「重み」と解釈できます。
– この重みを解釈しやすくするために、各共変量は平均が0、標準偏差が1に標準化されます。標準化された共変量に対する係数は、正準重み(canonical weight)と呼ばれています。正準重みが大きいほど、その共変量と正準変数との関係が大きいことを示します。
– バイプロット線の長さと方向は、最初の2次元までの正準変数に対する重みを表しています。バイプロット線の長さは、正準重みのノルムに比例しています。
– また、バイプロット線は、原点(0,0)を出発点としています。この原点は、全体平均を示しています。
– 重みの数値を知るには、「判別分析」の赤い三角ボタンのメニューから[正準オプション]>[正準の詳細を表示]を選択してください。そして、「正準の詳細」レポートの最下部で「標準化スコア係数」を開いてください。標準化スコア係数を参照してください。
正準プロットの編集
その他のオプションを使ってバイプロットを編集できます。
• 95%信頼楕円の表示/非表示は、「判別分析」の赤い三角ボタンのメニューから[正準オプション]>[平均の信頼限界楕円の表示]を選択して切り替えます。
• バイプロット線の表示/非表示は、「判別分析」の赤い三角ボタンのメニューから[正準オプション]>[バイプロット線の表示]を選択して切り替えます。
• バイプロット線の中心は、ドラッグして別の位置へ移動することができます。バイプロット線の位置およびスケールを指定するには、「判別分析」の赤い三角ボタンのメニューから[正準オプション]>[パイプロット線の位置]を選択します。正準プロットに表示されるデフォルトの半径のスケールは、調整しないとバイプロット線が見えない場合を除き、1.5です。
• 50%等高線の表示/非表示は、「判別分析」の赤い三角ボタンのメニューから[正準オプション]>[正規50%等高線の表示]を選択して切り替えます。
• 楕円と一致するように点を色分けするには、「判別分析」の赤い三角ボタンのメニューから[正準オプション]>[プロット点の色分け]を選択します。
3つ以上のカテゴリへの分類
「Iris.jmp」データの場合は3つの「種類」があるので、正準変数は2つだけです。Figure 5.7のプロットを見ると、2つの正準変数で3つのグループがいい具合に分かれていることがわかります。
プロット内のバイプロット線は、次のことを示しています。
• 「花弁の長さ」は、「正準1」と正の関連性があり、「正準2」と負の関連性があります。「正準2」よりも「正準1」での重みのほうが大きいです。
• 「花弁の幅」は、「正準1」と「正準2」の両方に正の関連性があります。これら2つの正準変数での重みは同じくらいです。
• 「がくの幅」は、「正準1」と負の関連性があり、「正準2」と正の関連性があります。「正準1」よりも「正準2」での重みのほうが大きいです。
• 「がくの長さ」は、「正準1」と負の関連性があり、「正準2」との関連性はほとんどありません。
2つのカテゴリへの分類
分類変数の水準が2つだけの場合、第1次元の正準変数(「正準1」)だけに点がプロットされます。各共変量の正準重みは「正準1」とだけに関連があります。バイプロット線の縦軸(「正準2」)における座標は、特に意味がありません。横軸(「正準1」)にバイプロット線を射影して、第1次元の正準変数における座標を見てください。
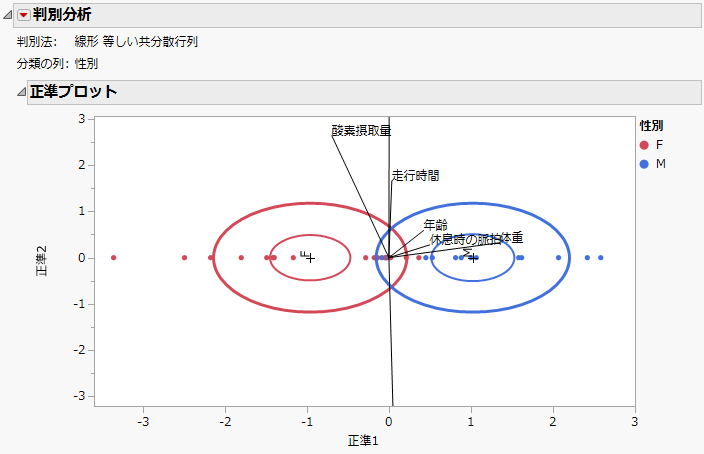
Figure 5.8は、「Fitness.jmp」サンプルデータの正準プロットです。被験者をM(男性)とF(女性)のカテゴリに分類するために、7つの連続変数が使われています。分類変数には2つのカテゴリしかないので、正準変数は1つだけです。
図5.8 「Fitness.jmp」の正準プロット
この正準プロットの点は、「性別」で色分けされています。2つのグループが「正準1」の値ではっきりと分かれていることに注目してください。
7つの共変量に対応するバイプロット線には縦軸方向にも成分がありますが、この場合は、「正準1」軸へ射影した座標だけを解釈しなければなりません。次のことを確認してください。
• 「最大脈拍」・「走行時間」・「走行時の脈拍」は、「正準1」とあまり関連がありません。
• 「体重」・「休息時の脈拍」・「年齢」は、「正準1」と正の関連があり、このうち「体重」が最も関連が強いです。共変量「休息時の脈拍」と「年齢」は、「正準1」との関連が弱いです。
• 「酸素摂取量」は、「正準1」と負の関連性があります。