比較
「寿命の二変量」レポートの「比較」セクションは、「ノンパラメトリック」重ね合わせプロットにて選択した分布の各種プロファイルが表示されます。次のタブがあります。
• 分布
• 分位点
• ハザード
• 密度
• 加速係数
• 比較の規準
ある確率分布のプロファイルを表示するには、「ノンパラメトリック」レポートにて、その確率分布のチェックボックスをオンにします。
プロファイル
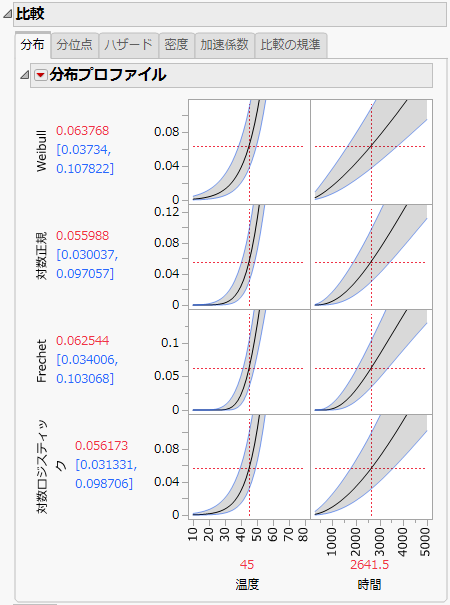
最初の5つのタブには、選択した確率分布のプロファイルが表示されています。最初の4つのプロファイルに表示される曲線は、それぞれ故障時間と加速因子（説明変数）の関数になっています。なお、［加速係数］タブの曲線は、加速因子（説明変数）だけの関数です。Figure 4.8は、Weibull・対数正規・Fréchet・対数ロジスティックの各確率分布に対する「分布プロファイル」です。
図4.8 分布プロファイル
［分位点］・［ハザード］・［密度］の各タブにも同様の結果が表示されます。「分布プロファイル」・「分位点プロファイル」・「ハザードプロファイル」・「密度プロファイル」・「加速係数プロファイル」は、他のプラットフォームで作成される予測プロファイルと似ています。たとえば、「温度」と「時間」の縦の線をドラッグすれば、温度と時間を変更したときの分布の値の変化を調べることができます。「予測プロファイル」については、『プロファイル機能』のプロファイルに詳しい説明があります。
分位点
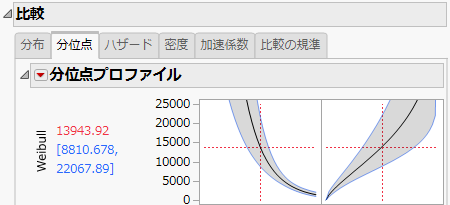
「分位点プロファイル」は、故障時間を外挿するのに役立ちます。データにWeibull分布をあてはめた場合を考えてみましょう。Figure 4.10のWeibull分布の加速係数プロファイルを見ると、使用条件の温度が10℃のときの45℃における加速係数は17.42132であることがわかります。［分位点］タブを選択して、Weibull分布の「分布プロファイル」を表示します。プロットでは、確率が0.5になる位置に縦線があります。Figure 4.9では、確率が0.5に設定されており、45℃における故障確率0.5の分位点は、13943.92時間であることがわかります。これらのことから、温度が10℃の場合、ユニットのうち50パーセントが故障する時間は、13943.92 × 17.42132 = 約242921時間であると推定できます。
図4.9 Weibull分位点プロファイル
加速係数
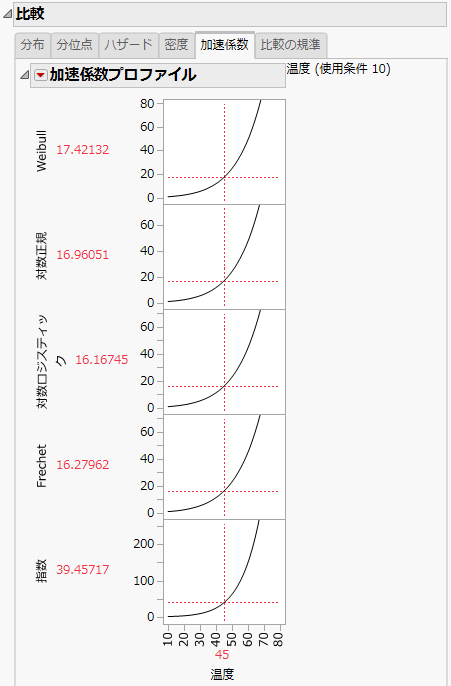
［加速係数］タブを選択すると、あてはめたすべての確率分布において、故障時間に対する「加速係数プロファイル」が表示されます。Figure 4.10を表示するには、「寿命の二変量」の赤い三角ボタンのメニューから［すべての分布のあてはめ］を選択します。加速係数を求めるときの説明変数の使用条件の値を変更するには、「寿命の二変量」の赤い三角ボタンのメニューから［使用条件の設定］を選択して、任意の値を入力します。説明変数と使用条件の値は、「加速係数プロファイル」というタイトルの横に表示されます。
図4.10 加速係数プロファイル
加速係数プロファイルでの数値をもとに、パラメトリックな分布を仮定した場合の、使用条件と比較したときの加速試験条件での故障時間を算出することができます。「加速係数」は、多くの場合、使用条件におけるpパーセント点と加速試験条件におけるpパーセント点の比です。対数正規分布・Weibull分布・対数ロジスティック分布・Fréchet分布において、加速因子のどの水準でも尺度パラメータが同じである場合に、このような関係が成立します。確率分布についての詳細は、確率分布の統計的詳細を参照してください。
メモ: 説明変数が離散値を取る場合や離散変数として扱われた場合、または、カスタマイズした計算式によって一定でない尺度パラメータが指定された場合、または、分布として正規分布・最小極値分布・ロジスティック分布・最大極値分布が指定された場合には、加速係数プロファイルは表示されません。
比較の規準
［比較の規準］タブには、あてはめた分布に対して、(-2)* 対数尤度・AICc・BICの各規準が表示されます。Figure 4.11に、Weibull・対数正規・対数ロジスティック・Fréchetの各分布に対する結果を示します。データへのあてはまりの良い分布が「比較の規準」表の一番上に表示されます（「AICc」を基準に並べ替えられます）。
図4.11 分析レポートの［比較の規準］タブ
このレポートを見ると、対数正規分布と対数ロジスティック分布の規準値が小さいことから、最もよくあてはまっている分布はこれらの確率分布であると結論できます。規準の詳細については、『基本的な回帰モデル』の尤度・AICc・BICを参照してください。