判別分析の手法

「判別分析」プラットフォームでは、判別分析の手法として、線形判別分析・2次判別分析・正則化判別分析、そして、横長データに対する線形判別分析を行えます。最初の3つの手法は、仮定されているモデルが異なります。［横長データ］の手法も線形判別モデルをあてはめるのですが、共変量の数が多い状況において効率的に計算が行われます。

メモ: 500個以上の共変量を追加すると、横長データの手法への変更を促す警告が表示されます。列数が非常に多い場合に通常の方法を使用すると、計算に時間がかかるためです。横長データの手法に変更する場合は、［線形 横長データ］をクリックしてください。すでに選択している手法を使用する場合は、［続行］をクリックします。

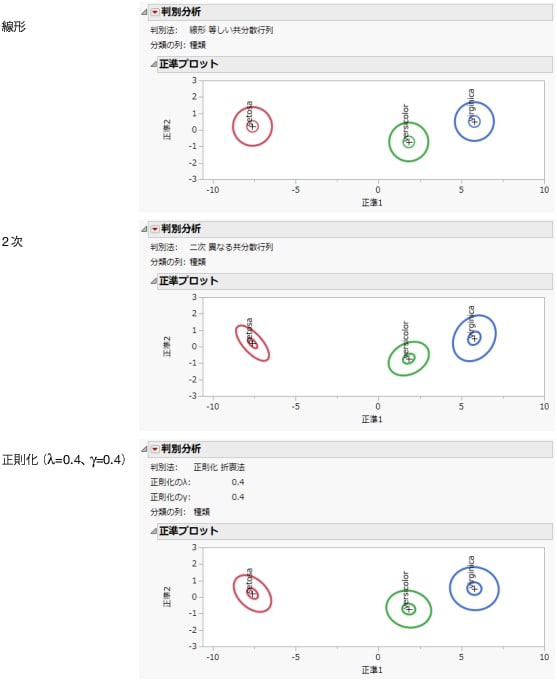
図5.5 線形・2次・正則化の判別法 

［線形］・［2次］・［正則化］の判別法をFigure 5.5に示します。以下に、これらの手法について概説します。詳細については、保存される計算式に関する統計的詳細を参照してください。

線形 等しい共分散行列

線形判別分析を実行します。この手法では、群内共分散行列（グループ内共分散行列）がすべて等しいと仮定されます。線形判別法を参照してください。

2次 異なる共分散行列

2次判別分析を実行します。この手法では、群内共分散行列がすべて異なると仮定されます。この手法では、共分散行列を推定するのに、線形法の場合よりも多くのパラメータを推定しなければいけません。ある群の標本サイズが小さい場合、推定値が不安定になってしまう危険があります。2次判別法を参照してください。

あるグループ内で値がすべて同じ共変量が存在していると、その共変量との共分散がすべて0になります。このような状況でも群内共分散行列の逆行列を求めるため、0となっている共分散が、プールして計算された共分散に置き換えられます。この処理が行われたときは、レポートウィンドウに該当する共変量と群を示すメモが表示されます。

ヒント: 2次判別分析は、小規模なデータセットには適していません。逆行列が計算できなかったり、安定した共分散行列が得られなかったりします。このような問題を改良し、データが足りない場合でもグループ間で異なる共分散行列を仮定できるのが、正則化の手法です。

正則化 折衷法

この手法でも群内共分散行列がすべて異なると仮定されますが、より安定した推定値を導き出すために2つの調整方法が用意されています。この手法は、グループの標本サイズが小さいときに役立ちます。正則化 折衷法および正則化判別法を参照してください。

線形 横長データ

共変量の数が多くて、他の手法では計算が難しい場合に役立ちます。この手法では、郡内共分散行列がすべて等しいと仮定されます。この手法は、プールした群内共分散行列の逆行列を計算するのに、特異値分解を用います。［線形 横長データ］のアルゴリズムの統計的詳細を参照してください。

メモ: ［線形 横長データ］オプションを使用した場合、他の判別法では用意されている機能の一部が使用できません。その理由は、横長データの場合にはプールした群内共分散行列が巨大になりますが、このアルゴリズムではその巨大な群内共分散を明示的に計算しないためです。

正則化 折衷法

正則化判別分析は、負でないパラメータを2つ使います。

• 最初のパラメータ（「λ: 共通の共分散行列に近づける度合い」）は、個別の共分散行列と共通の共分散行列をどのように混合するかを示します。このλ（ラムダ）が1のときは線形判別、0のときは2次判別に該当します。

• 第2のパラメータ（「γ: 対角行列に近づける度合い」）は、非対角要素、つまり変数間での共分散を収縮させる度合いを示します。γ（ガンマ）を1にすると、共分散行列が対角行列になります。

λおよびγを両方とも0に指定した場合は、2次判別分析と同じ結果になります。同様に、λを1、γを0に指定した場合は、線形判別分析と同じ結果になります。正則化を指定する際、Table 5.1を参考にしてください。線形判別分析・2次判別分析・正則化判別分析の例については、Figure 5.5を参照してください。