連続変数の分布
連続変数を分析するときには、必要に応じて、分布の形や平均などを検討します。
• データの分布形状が既知の分布に一致しているか
• 外れ値の有無
• データの平均はどれぐらいか
• 平均が、目標値(もしくは過去の値)と統計的に異なっているか
• データはどれぐらいばらついているか。標準偏差はどれぐらいか
• 最小値と最大値はどれぐらいか
上記のような疑問については、グラフ、要約統計量、統計的検定によって回答を導き出せます。
シナリオ
この例では、自動車のサンプルデータ「Car Physical Data.jmp」を使用します。このデータには、116車種の自動車の車両情報が記録されています。
プラニング専門家が鉄道会社から依頼を受け、鉄道による自動車輸送時の問題について検討することになりました。データに基づいて、次の点を調査する必要があります。
• 車両の平均重量
• 車両重量のばらつき(標準偏差)
• 車両の最小重量と最大重量
• 外れ値の有無
回答を導き出すために、車両重量のヒストグラムを描きます。
ヒストグラムの作成
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Car Physical Data.jmp」を開きます。
2. [分析]>[一変量の分布]を選択します。
3. 「車両重量」を選択し、[Y, 列]をクリックします。
4. [OK]をクリックします。
5. レポートウィンドウの内容を横に並べるには、「車両重量」の横にある赤い三角ボタンをクリックし、メニューから[表示オプション]>[横に並べる]を選択します。
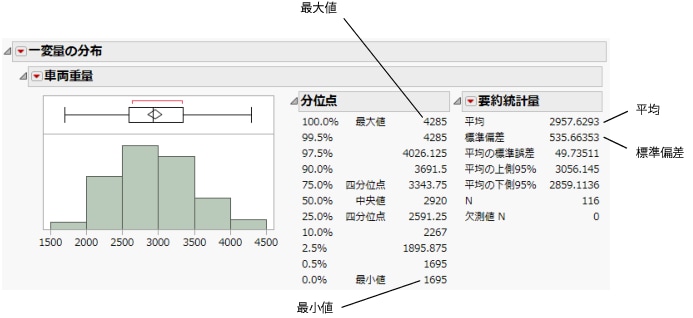
図5.7 「車両重量」の一変量の分布
レポートウィンドウには次の結果があります。
• ヒストグラムと箱ひげ図でデータが視覚化されます。
• 「分位点」レポートには、分布のパーセント点が示されます。
• 「要約統計量」レポートには、平均や標準偏差などの統計量が表示されます。
結果の解釈
Figure 5.7に示されている結果から、次のことが分かります。
車両の平均重量
ヒストグラムから、車両の平均重量が約3,000ポンドであることがわかります。
車両重量のばらつき(標準偏差)
「要約統計量」レポートから、車両の平均重量が約2,958ポンドであることが分かります。また、同じ「要約統計量」レポートから、標準偏差が約536ポンドであることが分かります。
最小重量と最大重量
ヒストグラムから、最小重量が約1,500ポンドで、最大重量が約4,500ポンドであることがわかります。「分位点」レポートから、最小重量が約1,695ポンドで、最大重量が約4,285ポンドであることが分かります。
外れ値の有無
外れ値はありません。
デフォルトのレポートウィンドウ(Figure 5.7を参照)には、最小限のグラフと統計量しか表示されません。赤い三角ボタンで表示するメニューを使用して、他のグラフや統計量を追加できます。
統計的検定
他の研究結果から、平均重量が3000ポンドでない場合には輸送効率が低いと鉄道会社は判断しました。そこで、輸送される車両の母集団において、平均重量が3000ポンドかどうかを確認する必要が生じました。t検定によって、現在の標本から母集団について推論します。
検定の結果
1. 「車両重量」の赤い三角ボタンをクリックし、メニューから[平均の検定]を選択します。
2. 表示されたウィンドウで、「仮説平均を指定」ボックスに「3000」と入力します。
3. [OK]をクリックします。
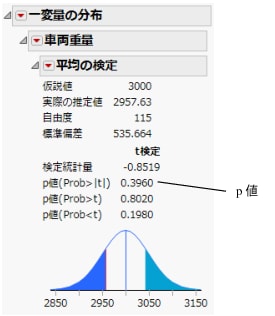
図5.8 平均の検定結果
t検定の解釈
t検定の主な結果はp値です。この例では、p値は0.396です。有意水準を0.05とした場合、0.396は0.05よりも大きいため、平均重量と3000 ポンドの間に統計的な有意差は認められませんでした。p値が有意水準よりも小さいときには、「母集団の平均車両重量は3000ポンドと異なる」という結論が導き出されます。