検出力の事前計算の例
この例では、シミュレーション機能を使って非線形モデルの検出力の事前計算を行います。6つの連続尺度の因子が、部品検査の合否におよぼす主効果を調べたいとしましょう。応答は二項分布に従い、実験は60回行えるものとします。
一般化線形モデルで、リンク関数としてロジット関数を使用して、成功確率をモデル化します。リンク関数としてロジット関数を使用すると、次のロジスティックモデルがあてはめられます。
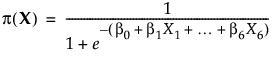
ここで、p(X)は、X = (X1, X2, ..., X6)という因子設定のもと、部品が合格する確率を表します。
線形予測子L(X)は、次の式で表されます。
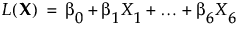
線形予測子の係数が次のような場合だったときの検出力を求めてみましょう。
|
係数 |
値 |
|---|---|
|
b0 |
0 |
|
b1 |
1 |
|
b2 |
0.9 |
|
b3 |
0.8 |
|
b4 |
0.7 |
|
b5 |
0.6 |
|
b6 |
0.5 |
線形予測子の切片は0なので、全因子が0に設定されている場合、部品が合格する確率は50%に等しくなります。第i因子の各水準における合格率は、その他の因子がすべて0である場合、次のようになります。
|
因子 |
Xi = 1の場合の合格率 |
Xi = -1の場合の合格率 |
差 |
|---|---|---|---|
|
X1 |
73.11% |
26.89% |
46.2% |
|
X2 |
71.09% |
28.91% |
42.2% |
|
X3 |
69.00% |
31.00% |
38.0% |
|
X4 |
66.82% |
33.18% |
33.6% |
|
X5 |
64.56% |
35.43% |
29.1% |
|
X6 |
62.25% |
37.75% |
24.5% |
たとえば、X1以外の全因子が0に設定されている場、検出したい差は46.2%になります。検出したい差が最小になるのは、X6以外の全因子が0に設定された場合で、その差は24.5%です。
計画の作成
ここでは、実験に対するカスタム計画を作成します。
メモ: この節の手順を省略するには、[ヘルプ]>[サンプルデータフォルダ]を選択し、「Design Experiment」フォルダの「Experiment.jmp」を開きます。「DOE シミュレート」スクリプトの横にある緑色の三角形をクリックし、[応答をシミュレート]の設定に進んでください。
1. [実験計画(DOE)]>[カスタム計画]を選択します。
メモ: カスタム計画は、非線形な状況に最適とはいえませんが、この例では、単純化するために、「非線形計画」プラットフォームではなく「カスタム計画」プラットフォームを使用します。「非線形計画」プラットフォームで作成した計画のほうが直交計画より優れていることを示す例については、『実験計画(DOE)』の非線形計画の例を参照してください。
2. 「因子」アウトラインで、「N個の因子を追加」の横のボックスに「6」と入力します。
3. [因子の追加]>[連続変数]を選択します。
4. [続行]をクリックします。
主効果だけの計画を作成したいため、「モデル」アウトラインには変更を加えません。
5. 「実験の回数」の「ユーザ定義」テキストボックスに「60」と入力します。
6. 「カスタム計画」の赤い三角ボタンをクリックし、メニューから[応答のシミュレート]を選択します。
この操作を行っておくと、[テーブルの作成]をクリックして計画のデータテーブルを作成したときに、「応答をシミュレート」ウィンドウが開きます。
メモ: 乱数シード値(step 7)と開始点の数(step 8)を設定すると、この例と同じ実験が得られます。同じ結果でなくても良い場合は、これらの手順は不要です。
7. (オプション)「カスタム計画」の赤い三角ボタンをクリックして、[乱数シード値の設定]を選択します。「12345」と入力して[OK]をクリックします。
8. (オプション)「カスタム計画」の赤い三角ボタンをクリックして、[開始点の数]を選択します。「1」と入力して[OK]をクリックします。
9. [計画の作成]をクリックします。
10. [テーブルの作成]をクリックします。
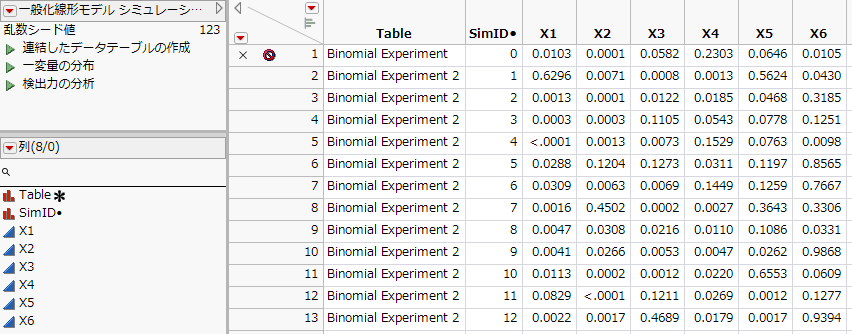
メモ: 乱数を用いているため、「Y」および「Yのシミュレーション」の値は、Figure 10.18とは異なったものになります。
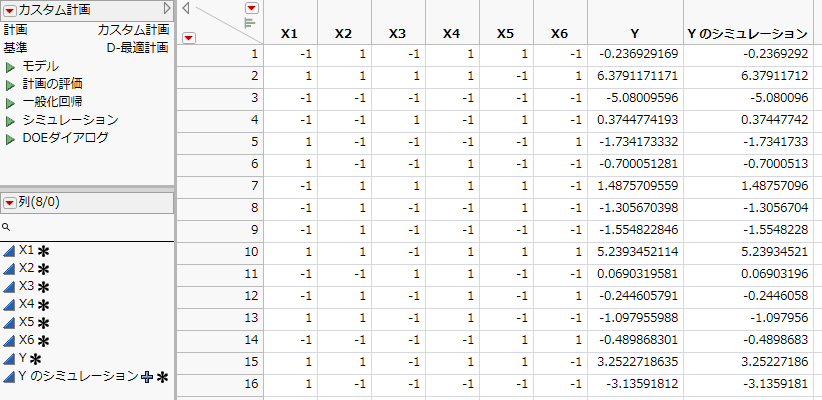
図10.18 計画テーブル(一部)
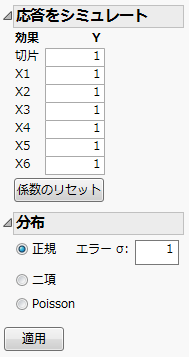
図10.19 「応答をシミュレート」ウィンドウ
計画のデータテーブルと「応答をシミュレート」ウィンドウが表示されます。計画のデータテーブルには、次の2つの列があります。
– 「Y」列: 「応答をシミュレート」ウィンドウの設定に従ってシミュレートされたデータ値。
– 「Yのシミュレーション」列: 計算式が含まれており、その計算結果が表示されている。「応答をシミュレート」ウィンドウでモデルを設定すると、そのモデルに従った乱数が生成されます。計算式を表示するには、「列」パネルで列名の右側にある+記号をクリックしてください。
次の節では、二項分布に従う応答をシミュレートして、一般化線形モデルをあてはめます。
[応答をシミュレート]の設定
ここでは、二項分布に従う応答データをシミュレートします。成功率はロジスティックモデルに従うものとします。[応答をシミュレート]の詳細については、『実験計画(DOE)』の応答のシミュレートを参照してください。
メモ: この節の手順を省略するには、「二項分布のシミュレート」スクリプトの横にある緑の三角ボタンをクリックします。この操作が済んだら、一般化線形モデルのあてはめに進んでください。
1. 「応答をシミュレート」ウィンドウ(Figure 10.19)で、「Y」の下に以下の値を入力します。
– 「切片」に「0」と入力します。
– 「X1」は、デフォルト値の「1」をそのまま使います。
– 「X2」に「0.9」と入力します。
– 「X3」に「0.8」と入力します。
– 「X4」に「0.7」と入力します。
– 「X5」に「0.6」と入力します。
– 「X6」に「0.5」と入力します。
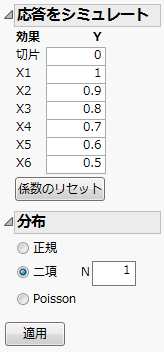
2. 「分布」アウトラインから[二項]を選択します。
「N」の値は「1」のままにしておきます。これは、それぞれの試行回数が1回だけであることを示します。
図10.20 設定後の「応答をシミュレート」ウィンドウ
3. [適用]をクリックします。
データテーブルの「Yのシミュレーション」列が、二項分布に従う乱数を生成する計算式に置き換えられます。「Y試行回数」の列には、各実験における試行回数が示されます。
4. (オプション)「列」パネルで、「Yのシミュレーション」の右側にある+記号をクリックします。
図10.21 「Yのシミュレーション」に挿入される、二項分布に従う乱数の計算式
5. [キャンセル]をクリックします。
一般化線形モデルのあてはめ
ここでは、一般化線形モデルを使って、ロジスティックモデルをあてはめます。
1. データテーブルの「モデル」スクリプトの横の緑の三角ボタンをクリックします。
2. [Y]ボタンの横の変数「Y」をクリックし、[削除]ボタンをクリックします。
3. 「Yのシミュレーション」をクリックし、[Y]ボタンをクリックします。
応答変数Yとして、二項分布に従う乱数の列が設定されます。
4. 「手法」リストから[一般化線形モデル]を選択します。
5. 「分布」リストから[二項]を選択します。
[リンク関数]メニューに[ロジット]が表示されます。
6. [実行]をクリックします。
二項分布のデータ1組に対して、モデルがあてはめられます。
検出力の考察
この例の冒頭で、線形予測子および係数と、係数によって決められる確率を示しました。ここでは、尤度比検定のp値をシミュレートして、それらの係数に対する検出力を調べます。
1. 「効果の検定」アウトラインで、「p値(Prob>ChiSq)」列を右クリックして[シミュレーション]を選択します。
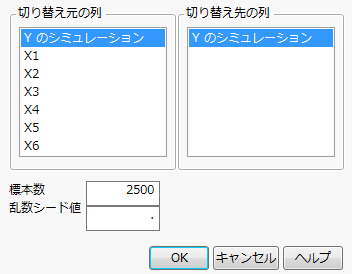
図10.22 「シミュレーション」ウィンドウ
「切り替え元の列」リストで[Yのシミュレーション]列が選択されていることを確認します。この列は、モデルのあてはめに使用されたデータ値を含んでいます。「切り替え先の列」でも「Yのシミュレーション」を選択すると、切り替え元の「Yのシミュレーション」データ値を、「Yのシミュレーション」の計算式で指定されている乱数に置き換えて、シミュレーションが実行されます。
レポートで選択した「p値(Prob>ChiSq)」列は、「係数がゼロである」という帰無仮説に対する尤度比検定のp値です。「効果の検定」表にある、各効果に対するこの「p値(Prob>ChiSq)」をシミュレートしましょう。
2. 「標本数」に「500」と入力します。
3. [OK]をクリックします。
「一般化線形モデル シミュレーション結果」データテーブルが表示されます。
メモ: シミュレーションは乱数によって行われるため、結果はFigure 10.23とは異なる可能性があります。
図10.23 「シミュレーション結果」テーブル(一部)
テーブルの最初の行は、観測されたデータから得られた「p値(Prob>ChiSq)」であり、除外の状態になっています。2行目以降の500行は、シミュレーションしたデータから計算された結果です。
4. 「検出力の分析」スクリプトを実行します。
メモ: 応答値はシミュレートされた乱数であるため、検出力のシミュレーションの結果は、Figure 10.24とは異なる可能性があります。
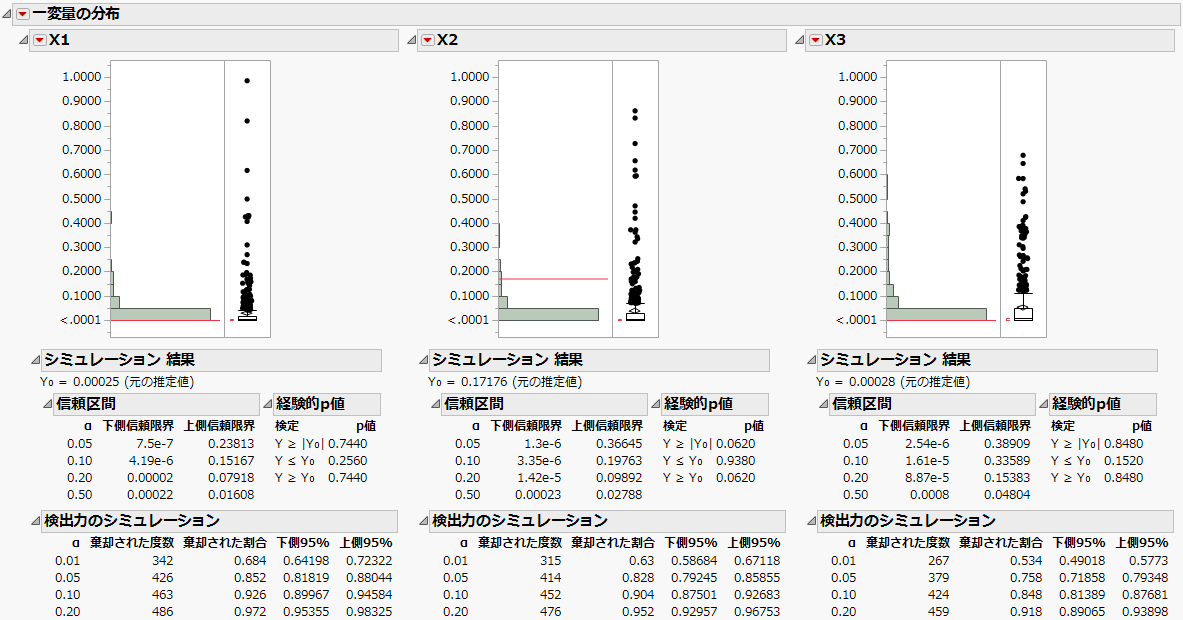
図10.24 一変量の分布(最初の2つの効果)
各主効果のヒストグラムには、シミュレーションによって得られた500個の「p値(Prob>ChiSq)」が描かれています。また、「検出力のシミュレーション」アウトラインには、500回のシミュレーションのうち有意性検定で棄却されたものの割合が表示されます。
次に、見やすくするために、レポートを縦に積み重ねて、プロットを非表示にしてみましょう。
5. 「一変量の分布」の赤い三角ボタンをクリックし、[積み重ねて表示]を選択します。
6. Ctrlキーを押しながら、「X1」の赤い三角ボタンをクリックし、[外れ値の箱ひげ図]の選択を解除します。
7. Ctrlキーを押しながら「X1」の赤い三角ボタンをクリックし、[ヒストグラムオプション]を選択し、[ヒストグラム]の選択を解除します。
メモ: 応答値はシミュレートされた乱数であるため、検出力のシミュレーションの結果は、Figure 10.25とは異なる可能性があります。
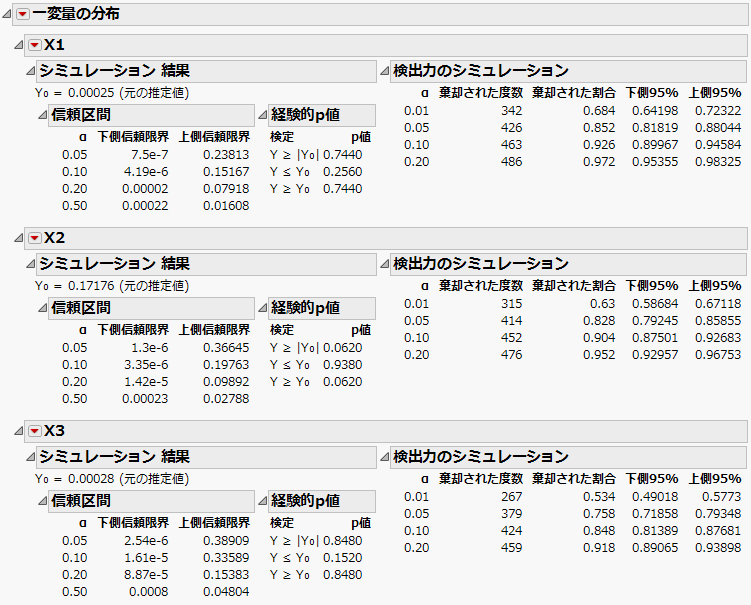
図10.25 検出力(最初の3つの効果)
「検出力のシミュレーション」アウトラインの「棄却された割合」は、シミュレーションのうち、p値がαより小さくなったものの割合を示します。たとえば、係数が0.8、確率の差が38%である「X3」で、棄却された割合を見てみると、有意水準0.05の検定で379/500 = 0.758となっています。Table 10.1は、シミュレーションで計算された、有意水準0.05の検定に対する検出力を、効果ごとに示したものです。「検出したい差」が小さくなるにつれ、検出力も小さくなっています。たとえば、「検出したい差」が24.5%(X6)における検出力は、約0.37にとどまっています。
メモ: 応答値はシミュレートされた乱数であるため、検出力のシミュレーションの結果は、Table 10.1とは異なる可能性があります。
因子 | Xi = 1の場合の合格率 | Xi = -1の場合の合格率 | 検出する差 | シミュレーションで得られた検出力(α=0.05で棄却された割合) |
|---|---|---|---|---|
X1 | 73.11% | 26.89% | 46.2% | 0.852 |
X2 | 71.09% | 28.91% | 42.2% | 0.828 |
X3 | 69.00% | 31.00% | 38.0% | 0.758 |
X4 | 66.82% | 33.18% | 33.6% | 0.654 |
X5 | 64.56% | 35.43% | 29.1% | 0.488 |
X6 | 62.25% | 37.75% | 24.5% | 0.372 |