傾きが異なる共分散分析の例
「モデルのあてはめ」プラットフォームの[標準最小2乗]手法を使って、傾きが異なる共分散分析を行います。この例では、名義尺度の変数の水準ごとに回帰直線の傾きが異なるモデルをあてはめてみましょう。モデルにあてはめた後、説明変数の特定の値で、名義尺度の変数の水準の最小2乗平均を比較します。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Drug.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「y」を選択し、[Y]をクリックします。
4. 「薬剤」と「x」の両方を選択し、[マクロ]>[設定された次数まで]をクリックします。
これにより、「次数」ボックスで指定した次数までの項がモデルに追加されます。「次数」のデフォルト値は2です。これで、「薬剤」と「x」の主効果と、それらの交互作用である「薬剤*x」がモデル効果のリストに追加されたはずです。
5. [実行]をクリックします。
以上のような指定によるモデルは、前節の傾きが等しい共分散分析モデルに、2つの変数(x4iとx5i)が追加したものになります。これは、共変量に対する傾きが「薬剤」の水準ごとに異なるモデルになります。追加される2つの変数は、「薬剤」のダミー変数に共変量を掛けたものです。モデル式は、次のようになります。
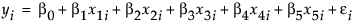
Table 4.1は、このモデルのコード変換を示しています。なお、交互作用項において、連続尺度の変数は、Xの平均10.7333を引くことにより、中心化されています。
|
説明変数 |
効果 |
値 |
|
x1 |
薬剤[a] |
aのとき+1、dのとき0、fのとき–1 |
|
x2 |
薬剤[d] |
aのとき0、dのとき+1、fのとき–1 |
|
x3 |
X |
Xの値 |
|
x4 |
薬剤[a]*(X - 10.733) |
aのときX – 10.7333、dのとき0、fのとき–(X – 10.7333) |
|
x5 |
薬剤[d]*(X - 10.733) |
aのとき0、dのときX – 10.7333、fのとき–(X – 10.7333) |
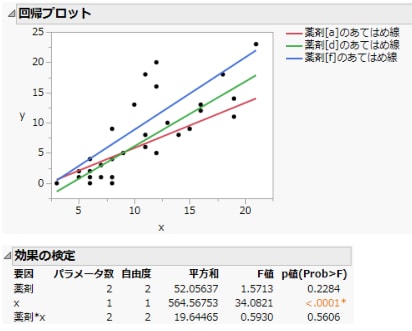
レポートの一部をFigure 4.6に示します。「回帰プロット」に描かれている回帰直線は、傾きが異なっており、平行にはなっていません。「効果の検定」レポートを見ると、交互作用のp値は0.56で、統計的には有意でありません。
図4.6 プロットと交互作用
スポットライト分析の実行
次に、共変量xの特定の値で「薬剤」の水準の最小2乗平均を比較します。共分散分析モデルなどにおけるこのような比較は、「スポットライト分析」と呼ばれることがあります。スポットライト分析の詳細については、Spiller et al.(2013)を参照してください。
1. 「応答 Y」の赤い三角ボタンをクリックし、[多重比較]を選択します。
2. 「多重比較」ウィンドウで、[ユーザ定義の推定値]を選択します。
3. [薬剤の水準を選択]の下の3つの値をすべて選択します。
4. xの下の最初のボックスに「12.5」と入力します。
5. [推定値の追加]をクリックします。
これは、3水準の[薬剤]をx = 12.5で比較したものを追加します。
6. [OK]をクリックします。
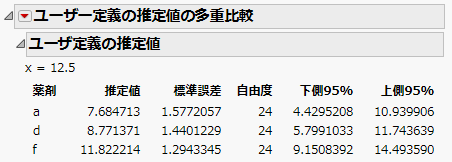
「ユーザ定義の推定値」レポートには、共変量xを12.5に設定した[薬剤]の各レベルの最小2乗平均の推定が表示されます。「ユーザ定義の推定値の多重比較」の横にある赤い三角形には、推定値の間の差を検定するオプションが含まれています。
図4.7 「ユーザ定義の推定値」レポート
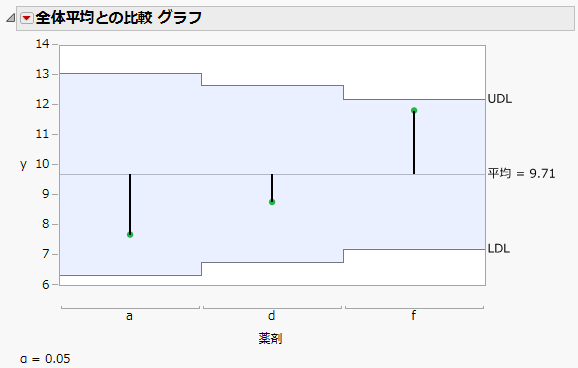
7. 「ユーザ定義の推定値の多重比較」の横にある赤い三角ボタンをクリックし、[全体平均との比較]を選択します。
図4.8 全体平均との比較 グラフ
[全体平均との比較]オプションでは、平均と3つの最小2乗平均との間の差に対する平均分析(ANOM; analysis of means)を作成します。平均分析(ANOM)のグラフにおいて、x = 12.5での全体平均からの差を見る限り、[薬剤]の統計的に有意な効果はありません。