競合原因分析の例
この例では、「生存時間分析」プラットフォームを使用して、複数の故障原因がある小さな電気製品の故障時間について調べます。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Reliability」フォルダにある「Appliance.jmp」を開きます。
2. [分析]>[信頼性/生存時間分析]>[生存時間分析]を選択します。
3. 「故障までの時間」を[Y, イベントまでの時間]に指定します。
4. [OK]をクリックします。
5. 「Kaplan-Meier法によるあてはめ」の赤い三角ボタンをクリックし、[競合する原因]を選択します。
6. 「原因コード」を選択し、[OK]をクリックします。
7. 「競合する原因」の赤い三角ボタンをクリックし、[ハザードプロット]を選択します。
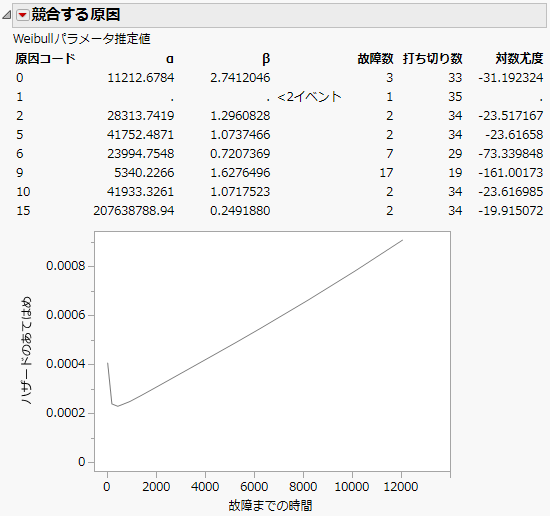
図14.11 「競合する原因」レポートとハザードプロット
システム全体の生存時間分布は、各故障原因の生存率の積で表わされます。「競合する原因」表には、故障原因ごとの、Weibull分布パラメータ(αとβ)の推定値が表示されます。
この例では、一番多い故障の原因が9であることがわかります。原因1は1回生じただけなので、適切なWeibull推定値が計算されませんでした。原因15は非常に短い時間で生じたため、αが大きく、βが小さくなっています。Weibull分布のαは尺度を表すパラメータであり、また、累積故障確率が63.2%に達する故障時間になっています。信頼性データ解析では、「特性寿命」とも呼ばれています。競合原因分析では、早い時点だけで故障が生じている原因は、αが非常に大きくなります。このような早い時点だけで故障が生じている原因は、早い時点で故障が生じていないものは、それ以降でこの原因で故障する可能性は低いとみなされるからです。
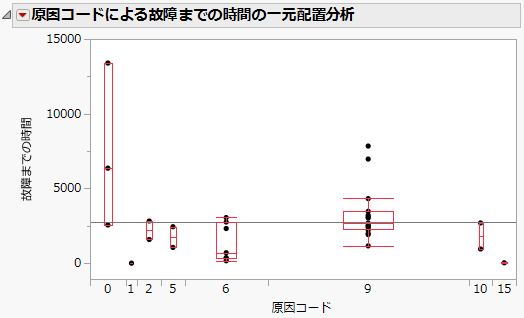
Figure 14.12は、「故障までの時間」と「原因コード」を「二変量の関係」でプロットして、分位点オプションを選択したものです。このプロットを見ると、αとβがどのように故障時間分布に関連するかがわかります。
図14.12 「二変量の関係」で作成した「故障までの時間」と「原因コード」
この例では、一番多い故障の原因が9であることがわかります。原因9を除去した場合、他の原因による生存時間分布はどのような影響を受けるでしょうか。[原因の削除]オプションを選択して原因の値を削除し、生存率の推定値を再計算します。
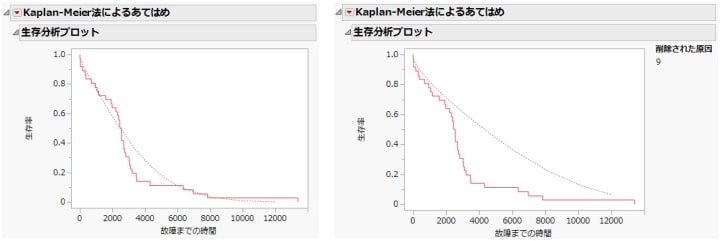
Figure 14.13は、競合する原因をすべて含めた生存時間プロットと原因9を除去した生存時間プロットです。原因9を除去したプロットを見ると、2,000時間までは生存率(点線)があまり改善されていませんが、その後は、10,000時間を超えても元のプロットよりずっと高い値を取り続けます。
図14.13 原因を削除したときの生存時間プロット