「時間ID」列の作成例
この例では、時間IDに適した新しい列を作成し、「時系列分析」プラットフォームを使用して分析を行います。
適切な「時間ID」列の作成
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Time Series」フォルダにある「SeriesP.jmp」を開きます。
「SeriesP.jmp」データテーブルには、応答を観測した期間を表す「年」列と「四半期」列があります。しかし、「時系列」プラットフォームのX軸には、等間隔で並んだ一意の時点を含む1つの列しか使えません。[時間ID]を指定しない場合は、自動的に行番号で代用されます。行番号では期間がわかりにくいため、「年」と「四半期」を使って時間ID列を作成しましょう。
2. [列]>[列の新規作成]を選択します。「列名」ボックスに、「年.四半期」と入力します。
3. 「表示形式」の横で[最適]>[日付]>[yyyyQq]と変更します。
4. [列プロパティ]>[計算式]を選択します。
5. 「日付時間」の横にあるグレーの三角ボタンをクリックし、[Informat]を選択します。
6. 「文字」の横にあるグレーの三角ボタンをクリックします。
7. 「年」を選択し、[Char]をクリックした後、[Concat]をクリックします。
8. ボックスに「“Q”」(引用符を含む)と入力し、Enterキーを押します。
9. [Concat]をクリックします。
10. 「四半期」を選択し、[Char]をクリックします。
11. 「<formatName>」ボックスをクリックし、「yyyyQq」と入力して、Enterキーを押します。
12. [OK]をクリックします。
設定し終わった「列の新規作成」ウィンドウはFigure 18.16のようになります。
図18.16 列の新規作成
13. [OK]をクリックします。
メモ: この時間列はX11分析にも使用できます。
時系列分析
データテーブルに適切な時間ID列ができたので、分析に進みます。
1. [分析]>[発展的なモデル]>[時系列分析]を選択します。
2. 「国内総生産」を選択し、[Y, 時系列]をクリックします。
3. 「年.四半期」を選択し、[X, 時間ID]をクリックします。
4. [OK]をクリックします。
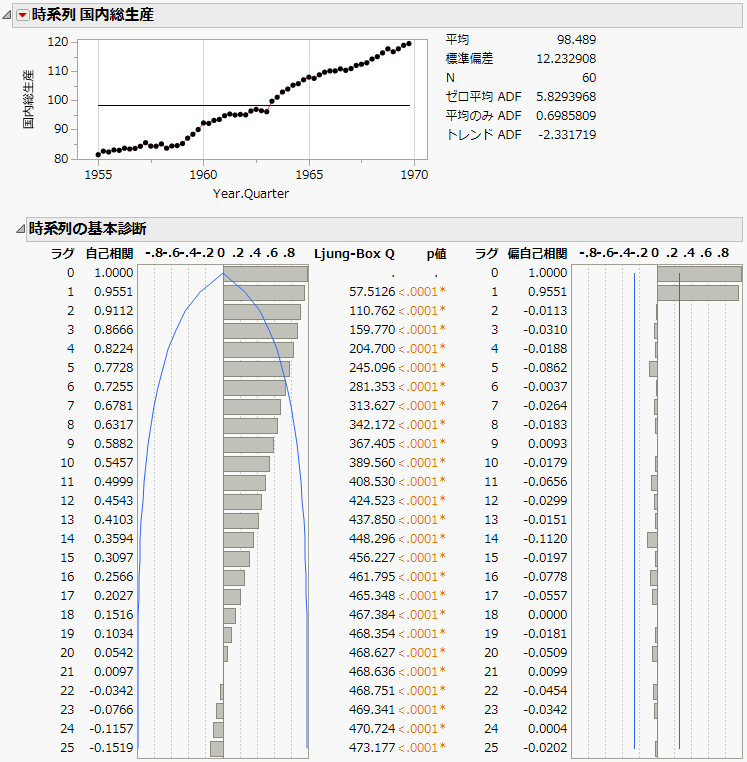
図18.17 「SeriesP.jmp」の「時系列」レポート
時系列には、線形に近い増加の傾向(トレンド)が見られます。さらに、自己相関プロットを見ると、時点が近い点の間には強い相関があることがわかります。ラグが1、2、3の点は、自己相関の値がそれぞれ0.9551、0.9112、0.8666です。
5. 「時系列 国内総生産」の赤い三角ボタンをクリックし、[差分]を選択します。
6. 季節性のない差分の次数を「1」に設定し、[推定]をクリックします。
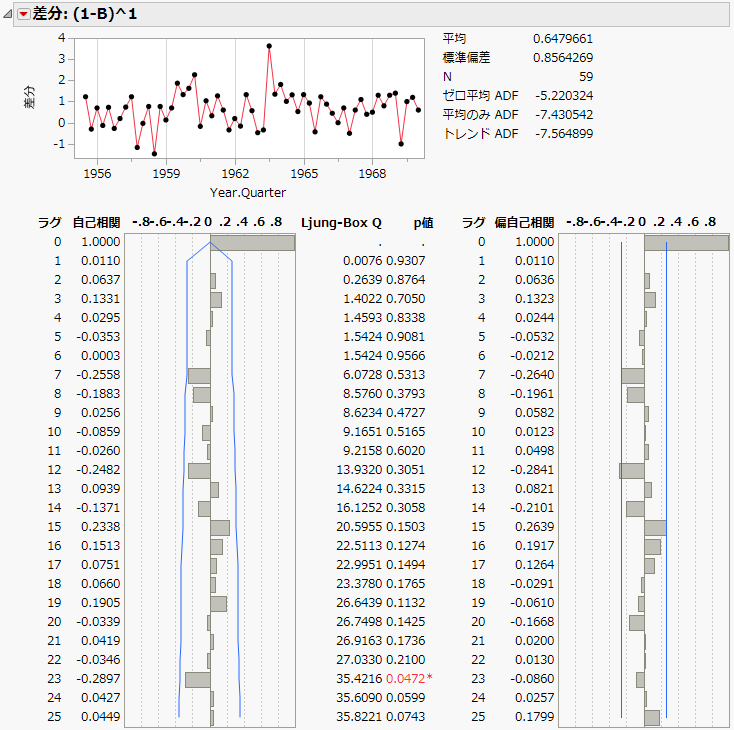
図18.18 「SeriesP.jmp」の「差分」レポート
「差分」レポートは、どのように差分をとるのが適しているかの判断に役立ちます。差分のプロットを見ると、差分を取った時系列には原系列で見られたような傾向(トレンド)がないことがわかります。そのため、ラグ1の差分が適切だと考えられます。また、トレンドの除外後も季節性の兆候は見られません。これらの理由から、原系列に対するモデルは、線形傾向(線形トレンド)を考慮する必要があるでしょう。また、季節性を考慮する必要はありません。よって、指数平滑化法やARIMAモデルが適切でしょう。
7. 「時系列 国内総生産」の赤い三角ボタンをクリックし、[平滑化法モデル]>[線形指数平滑化法]を選択します。
8. [推定]をクリックします。
9. 「時系列 国内総生産」の赤い三角ボタンをクリックし、[複数のARIMAモデル]を選択します。このオプションでは、(p,d,q)(P,D,Q)の値範囲で複数のARIMAモデルをあてはめることができます。
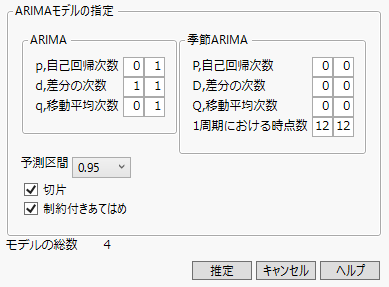
10. 「ARIMA」パネルで以下の範囲を設定します。
– 差分のレポートから、ラグ1の差分が適切だと考えられるため、差分の次数dを1に固定します。それには、範囲を1~1に設定します。
– 原系列に自己相関の証拠が見られたため、自己回帰次数pを0~1に設定します。
– 移動平均次数qを0~1に設定します。
メモ: ほとんどの場合、pとqには小さな値を指定しただけで十分です。
– 時系列には季節性の証拠が見られなかったため、P、D、Qは0のままにします。
このように設定すると、合計4つのモデルがあてはめられます。
図18.19 「複数のARIMAモデル」の指定ウィンドウ
11. [推定]をクリックします。
図18.20 モデルの比較
「モデルの比較」表は、AIC規準に従って最良と判断されたモデルから順に並んでいます。この例では、ARIMA(0,1,0)モデル(レポートでは「I(1)」と表記)が原系列に最もよくあてはまっています。「I(1)」モデルが「最良」にはなっていますが、どのモデルも適合度統計量に大きな差はありません。どれも適切だと考えることができます。
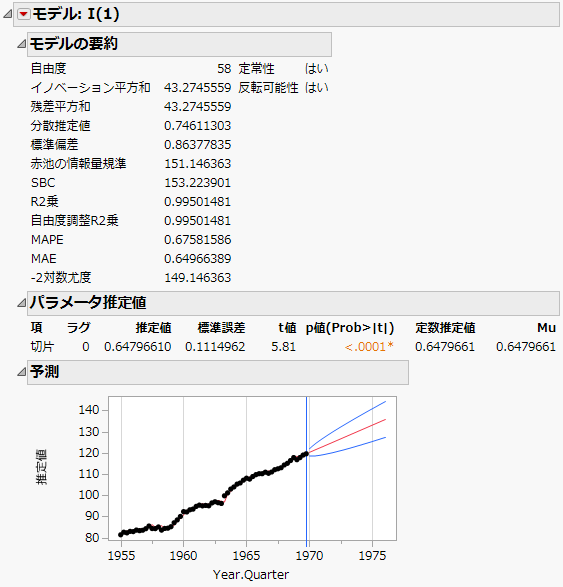
図18.21 ARIMA(0,1,0)のモデルレポート
「I(1)」のモデルレポートに予測グラフが表示されています。青色の線は予測区間を示します。「国内総生産」の予測値は線形的に増加しています。