正規分布の回帰モデルと対数リンクの例

この例では、応答の確率分布が正規分布で、リンク関数が対数である一般化線形回帰モデルをあてはめます。まず、説明変数と応答変数の関係を調べ、「モデルのあてはめ」プラットフォームの［一般化線形モデル］手法でどのリンク関数を使うのが適切かを特定します。

1. ［ヘルプ］>［サンプルデータフォルダ］を選択し、「Nor.jmp」を開きます。

2. ［分析］>［二変量の関係］を選択します。

3. 「Y」を選択し、［Y, 目的変数］をクリックします。

4. 「X」を選択し、［X, 説明変数］をクリックしてから［OK］をクリックします。

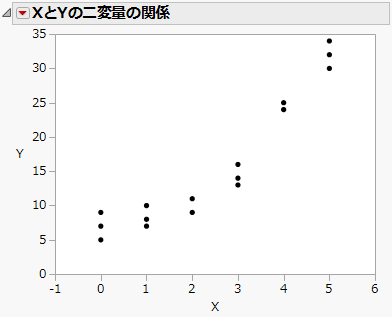
図13.8 二変量の関係 

YとXの関係が非線形であり、分散がほぼ一定であることがわかります。そこで、正規分布と対数リンク関数を使ってモデルをあてはめることにします。式は、log(mi) = xi'b、つまり、mi = exp(xi'b) です。

5. ［分析］>［モデルのあてはめ］を選択します。

6. 「手法」リストで［一般化線形モデル］を選択します。

7. 「分布」リストで［正規］を選択します。

8. 「リンク関数」リストで［対数］を選択します。

9. 「Y」を選択し、［Y］をクリックします。

10. 「X」を選択し、［追加］をクリックします。

11. ［実行］をクリックします。

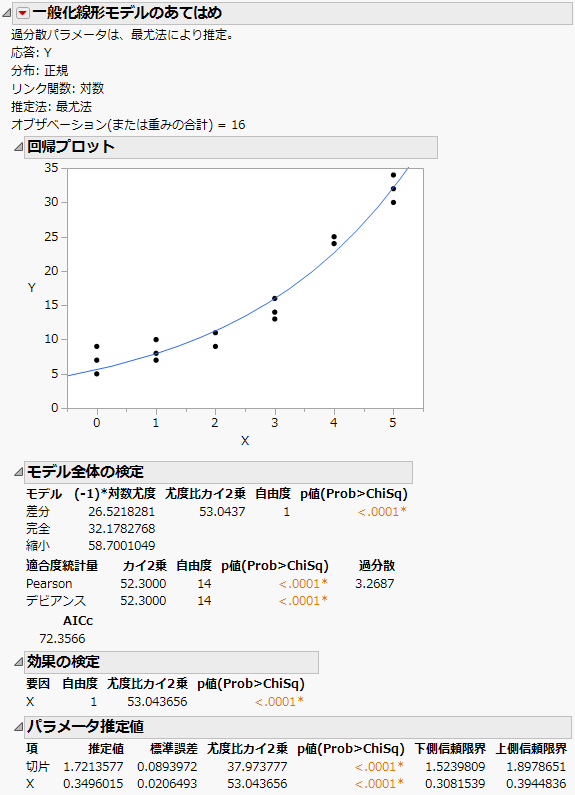
図13.9 モデルの結果