シミュレーション機能の例
変更が困難な変数の分散成分について、セミパラメトリックな信頼区間を計算してみましょう。この例では、温度、時間、触媒の量が、反応におよぼす効果を調べたいとします。温度は、変更が非常に困難な変数(一次単位因子)です。時間は、変更が困難な変数(二次単位因子)です。触媒の量は、変更が容易な変数です。一次単位因子と二次単位因子については、『実験計画(DOE)』の一次単位と二次単位の数を参照してください。
過去の研究から、一次単位と二次単位の標準偏差は、それぞれ、誤差の標準偏差の約2倍と約1.5倍であることが分かっています。JMPがデフォルトで求めている信頼区間は、Wald法による近似によるもので、分散成分の推定量が漸近的に正規分布に従うものとして算出されています。このWald法による近似は精度が悪く、信頼区間の幅は狭くなる傾向があります。ここでは、分散成分の標本分布をシミュレートで求めて、分位点に基づいて信頼区間を計算してみます。
計画の作成
ここでは、カスタム計画を使用して、2段分割計画を作成します。
ヒント: この節の手順を省略するには、[ヘルプ]>[サンプルデータフォルダ]を選択し、「Design Experiment」フォルダの「Catalyst Design.jmp」を開きます。そして、「Catalyst Design.jmp」データテーブルの「DOEシミュレート」スクリプトの横にある緑の三角ボタンをクリックします。この操作が済んだら、モデルのあてはめに進んでください。
1. [実験計画(DOE)]>[カスタム計画]を選択します。
2. 「因子」アウトラインで、「N個の因子を追加」の横のボックスに「3」と入力します。
3. [因子の追加]>[連続変数]を選択します。
4. 因子の名前をダブルクリックして、「温度」、「時間」、「触媒」に変更します。
値は、デフォルトの「-1」と「1」をそのまま使用します。
5. 「温度」の[容易]をクリックして、[非常に困難]に変更します。
これで、「温度」が一次単位因子になります。
6. 「時間」の[容易]をクリックして、[困難]に変更します。
これで、「時間」が二次単位因子になります。
7. [続行]をクリックします。
8. 「モデル」パネルで[交互作用]>[2次]を選択します。
すると、モデルにすべての2次交互作用が追加されます。
9. 「カスタム計画」の赤い三角ボタンをクリックし、メニューから[応答のシミュレート]を選択します。
この操作を行っておくと、[テーブルの作成]をクリックして計画のデータテーブルを作成したときに、「応答をシミュレート」ウィンドウが開きます。
メモ: 乱数シード値(step 10)と開始点の数(step 11)を設定すると、以下の数値例と同じ実験設定が得られます。同じ結果でなくても良い場合は、これらの手順は不要です。
10. (オプション)「カスタム計画」の赤い三角ボタンをクリックして、[乱数シード値の設定]を選択します。「12345」と入力して[OK]をクリックします。
11. (オプション)「カスタム計画」の赤い三角ボタンをクリックして、[開始点の数]を選択します。「1000」と入力して[OK]をクリックします。
12. [計画の作成]をクリックします。
13. [テーブルの作成]をクリックします。
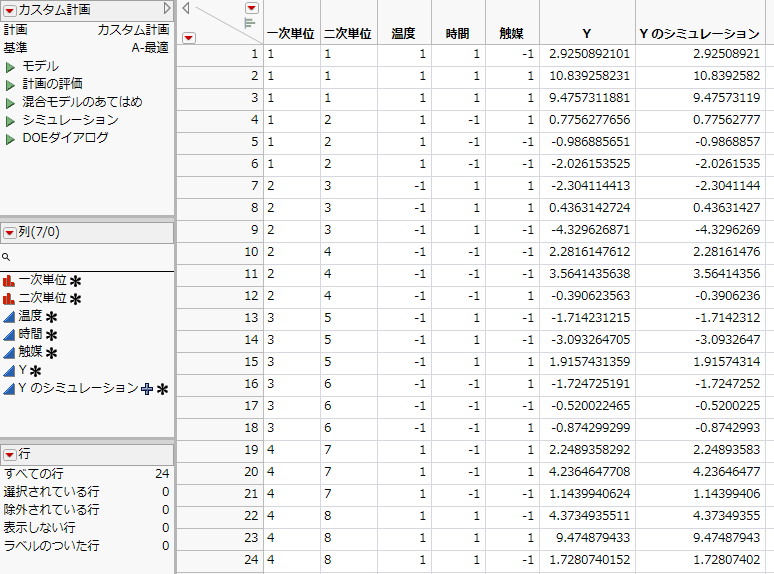
メモ: 乱数を用いているため、「Y」および「Yのシミュレーション」の値は、Figure 10.2とは異なったものになります。
図10.2 計画テーブル
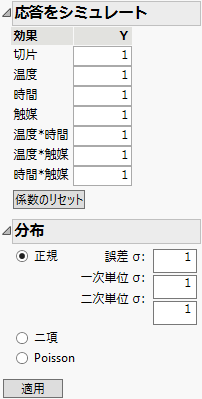
図10.3 「応答をシミュレート」ウィンドウ
計画のデータテーブルと「応答をシミュレート」ウィンドウが表示されます。データテーブルには、「シミュレーション」スクリプトが含まれています。このスクリプトを実行すれば、いつでもパラメータ値を変更できます。
次の節では、一次誤差と二次誤差の標準偏差を指定します。その後、乱数シミュレーションによって生成したデータに対して、REMLモデルをあてはめます。
モデルのあてはめ
ここでは、REML法を使ってモデルをあてはめます。一次誤差と二次誤差は、正規分布に従うと仮定します。また、誤差の標準偏差を1.0とした場合、一次誤差の標準偏差は2.0、二次誤差の標準偏差は1.5になっていると仮定します。一次単位と二次単位のばらつきにのみ興味がある場合は、「応答をシミュレート」ウィンドウにおける「効果」の数値は特に変更しなくてかまいません。
1. 「分布」パネル(Figure 10.3)の「一次単位 s」に「2」と入力します。
デフォルトで正規分布が選択されていることに注意してください。これにより、正規分布に従う誤差が計算式に追加されます。
2. 「二次単位 s」に「1.5」と入力します。
3. [適用]をクリックします。
データテーブルの「Yのシミュレーション」の計算式が更新されます。計算式を表示するには、「列」パネルで列名の右側にある+記号をクリックしてください。
4. データテーブルの「モデル」スクリプトの横の緑の三角ボタンをクリックします。
5. [Y]ボタンの横の変数「Y」をクリックし、[削除]ボタンをクリックします。
6. 「Yのシミュレーション」をクリックし、[Y]ボタンをクリックします。
これにより、「Y」が、シミュレーションの計算式を含む列に置き換えられます。
7. [実行]をクリックします。
シミュレートした応答の値1組に基づき、モデルがあてはめられます。
メモ: 「Yのシミュレーション」は乱数によって生成された値であるため、ここまでの手順に沿って作成したレポートの結果はFigure 10.4とは異なる可能性があります。
図10.4 REML法のレポートとWald法の信頼区間
信頼区間の生成
ここでは、分散成分の推定値をシミュレートして、信頼区間を求めます。
1. 「REML法による分散成分推定値」アウトラインで、「分散成分」列を右クリックして、[シミュレーション]を選択します。
図10.5 「シミュレーション」ウィンドウ
このシミュレーションでは、現モデルの推定に用いた「Yのシミュレーション」列のデータ値が、シミュレーションごとに「Yのシミュレーション」列の計算式で生成される乱数に置き換えられます。右クリックして選択された「分散成分」列がシミュレーションされます。右クリックした「分散成分」列が強調表示され、この列が「パラメータ推定値」テーブルに表示されている各効果に対してシミュレーションされることを示します。
2. 「標本数」に「200」と入力します。
3. (オプション)「乱数シード値」に「456」と入力します。
この操作を行うと、1行目を除き、Figure 10.6と同じ値が生成されます。
4. [OK]をクリックします。
1行目の値は、Figure 10.6とは異なる可能性があります。
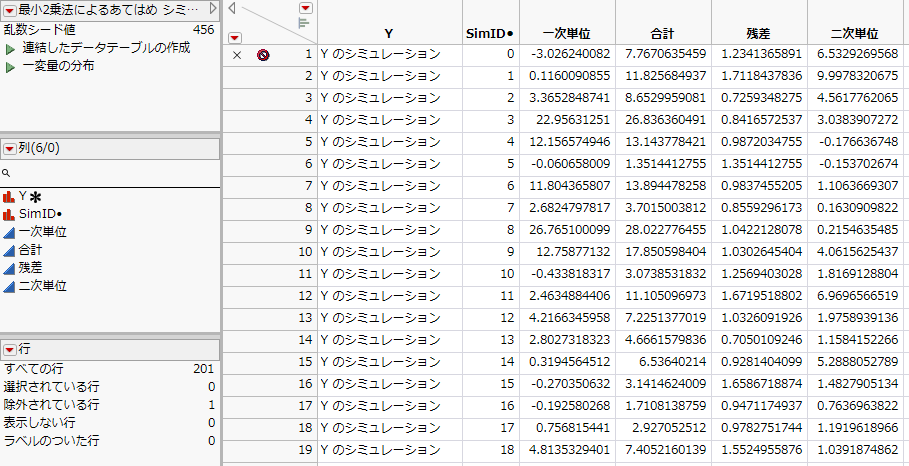
図10.6 分散成分のシミュレーション結果(一部)
「最小2乗法によるあてはめ シミュレーション結果(分散成分)」データテーブルの最初の行は、元データから計算された「分散成分」の推定値であり、除外の状態になっています。その他の行は、シミュレーションで生成された乱数です。
5. 「一変量の分布」スクリプトを実行します。
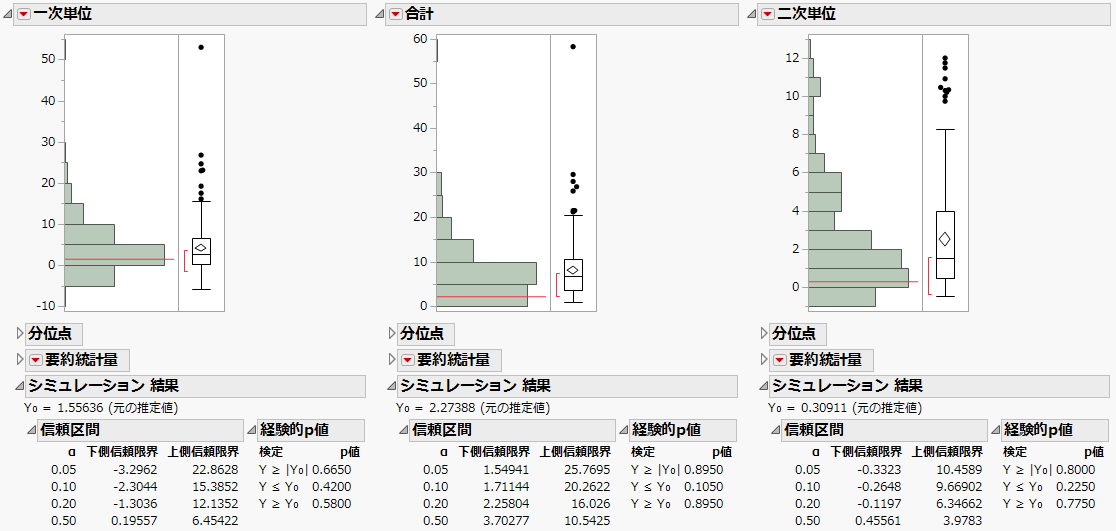
図10.7 分散成分に対して「一変量の分布」を実行した結果(一部)
各分散成分の信頼区間は、この「シミュレーション結果」レポートに示されているとおりです。α=0.05の行の95%信頼区間を、REMLレポート(Figure 10.4)の信頼区間と比較してみましょう。
– 一次単位の分散成分の95%信頼区間は、シミュレーションでは-3.296~22.863です。REMLレポートのWald法では、-1.973~5.086です。
– 二次単位の分散成分の95%信頼区間は、シミュレーションでは-0.332~10.459です。REMLレポートのWald法では、-0.605~1.223です。
シミュレーションによって求めた信頼区間は、1組の値を使ってREML法で計算した信頼区間に比べ、はるかに広くなっています。信頼区間の精度をさらに高めるには、シミュレーションの回数を増やしてみてください。