標準最小2乗法の使用例
この例では、「モデルのあてはめ」プラットフォームの[標準最小2乗]手法を使って、共分散分析モデルをあてはめます。薬効を調べるために、30名の患者に対して薬剤が無作為に割り付けられました。薬剤は3種類あり、データでは、「a」、「d」、および、プラセボ(偽薬)である「f」と記録されています。処置前後で患者の状態が測定され、処置前の値をx、処置後の値をyとしています。処置前の値xは、患者ごとの疾患の程度の違いを考慮するために、共変量としてモデルに含めるとします
これら3群で差があるかどうかを調べることが目的です。「y」を応答変数とし、「薬剤」、「x」、「薬剤」と「x」の交互作用を効果としたモデルをあてはめます。交互作用をモデルに含めたのは、疾患の程度によって、それぞれの薬剤の効果の大きさが異なるかもしれないからです(「モデルのあてはめ」の概略については、モデルの指定を参照してください)。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Drug.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「y」を選択し、[Y]をクリックします。
この列を[Y]として追加すると、「手法」が[標準最小2乗]になります。「強調点」オプションには[効果てこ比]が選択されますが、これは必要に応じて変更できます。
4. 「薬剤」と「x」を選択します。「列の選択」リストでこの2つの効果を強調表示したまま、[マクロ]をクリックして[完全実施要因]を選択します。この操作により、これら2つの効果と、これらの2因子間交互作用が「モデル効果の構成」リストに追加されます。
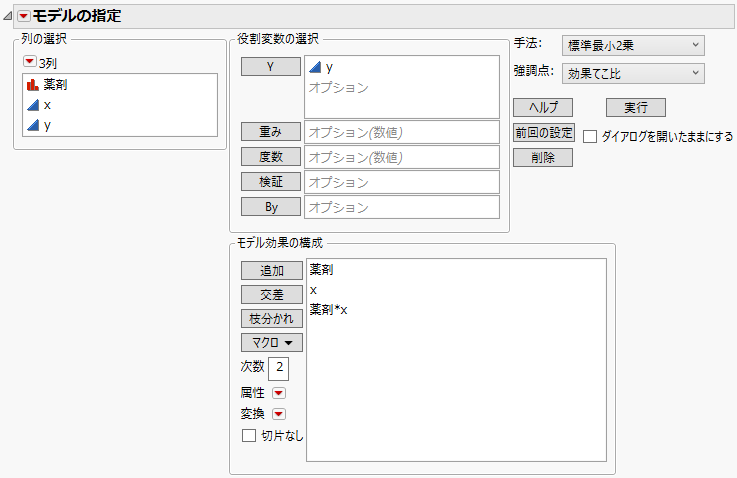
図3.2 入力が完了した「モデルのあてはめ」起動ウィンドウ
5. [実行]をクリックします。
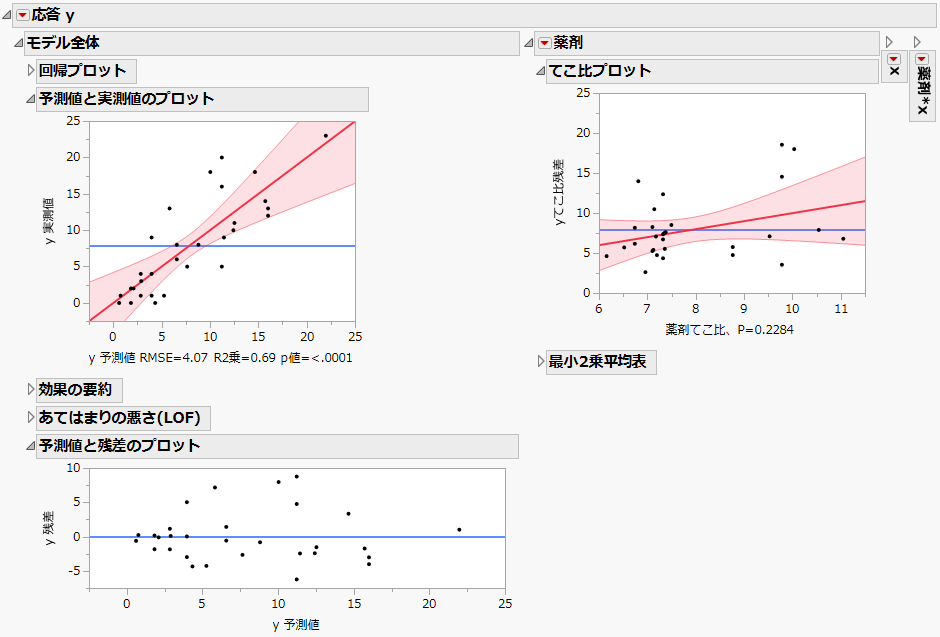
Figure 3.3に、「最小2乗法によるあてはめ」レポートを示します。なお、紙面の都合上、この図ではいくつかのレポートを閉じています。「予測値と実測値のプロット」、「予測値と残差のプロット」、および「てこ比プロット」を見ると、誤差などのモデルの前提に関して、データは矛盾していないようです。
図3.3 「最小2乗法によるあてはめ」レポート
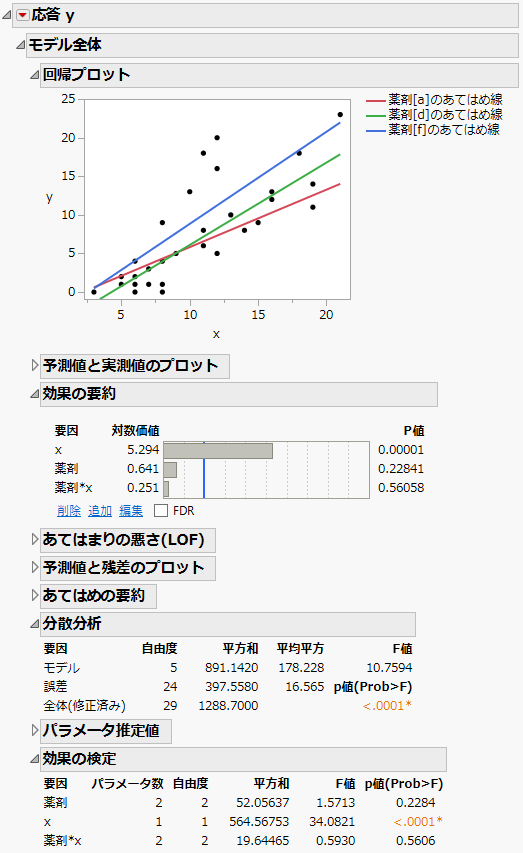
モデルの前提には明らかな問題がないようなので、次に検定を解釈していきましょう。Figure 3.4に、関連する検定結果を表示しています。まず、「分散分析」レポートを見てみると、モデル全体は統計的に有意です。
「回帰プロット」では、直線の傾きが異なっており、「薬剤」と処置前値「x」には交互作用があることが示唆されています。しかし、「効果の検定」レポートの「p値(Prob>F)」を見ると、交互作用項は統計的には有意ではありません。また、「x」は有意ですが、「薬剤」は有意ではありません。つまり、このデータからは、3群間の差は検出されませんでした。ただし、この検定結果から直ちに「薬剤には効果がない」と結論付けることはできません。実際には薬剤に何らかの効果があったのに、その効果を検出するのには、データの標本サイズが小さすぎただけかもしれません。
図3.4 「最小2乗法によるあてはめ」レポートでの検定結果