パラレルプロットの解釈

パラレルプロットを解釈する方法は、散布図と対比してみるとわかりやすくなります。以下の図では、左にパラレルプロット、右に散布図が表示されています。

強い正の相関

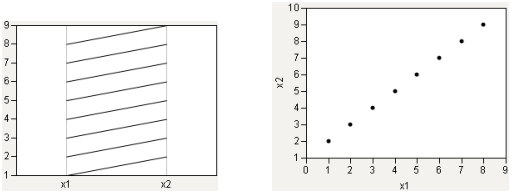
次の図は、強い正の相関をプロットしたものです。パラレルプロットの線がすべて同じ角度で傾斜してるのがわかります。

図7.6 強い正の相関 

強い負の相関

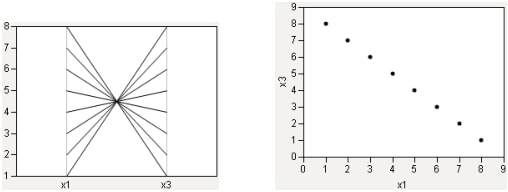
対照的に強い負の相関をプロットした場合は、パラレルプロットにくびれが生じます。

図7.7 強い負の相関 

共線性のあるグループ

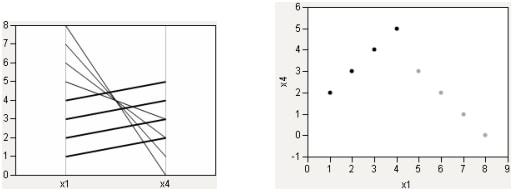
次に、両方の要素を持つケースを考えてみましょう。2つのグループがあり、どちらにも直線的な関係があります。一方は正の傾き、他方は負の傾きを持っています。Figure 7.8では、正の傾きを持つグループが強調表示されています。

図7.8 共線性のあるグループ: パラレルプロットと散布図 

外れ値が1つ

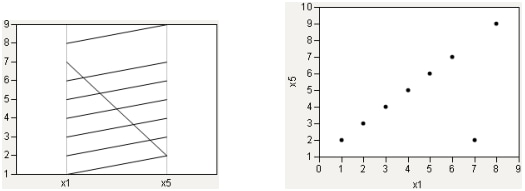
最後に、外れ値が1つあるケースを見てみます。パラレルプロットからは、多くの直線が一致した振る舞いをしていることと同時に、目立った例外も読み取れます。

図7.9 外れ値が1つ: パラレルプロットと散布図 

関連情報

• 「パラレルプロット」プラットフォームの別例