最適化基準
カスタム計画を作成するルーチンは、最適化基準によって異なります。ここでは、カスタム計画を作成するための最適化基準のオプションについて説明します。
• 推奨する最適化法
• D-最適化基準
• I-最適化基準
• A-最適化基準
• 交絡最適化基準
推奨する最適化法
JMPの「カスタム計画」では、主効果と交互作用だけの2水準計画にはA-最適化基準、[RSM]ボタンを使って生成した完全2次式モデルにはI-最適化基準、その他の計画にはD-最適化基準が、推奨する最適化基準に選ばれます。
D-最適化基準
D-最適化基準は、モデル係数に対する推定値の共分散行列の行列式を最小化します。つまり、D-最適計画は効果の推定値の推定精度に重点を置いています。次のような場合に適しています。
• スクリーニング計画
• 効果の推定もしくは有意性の検定に重点を置いた実験
• 重要な因子の特定を目的とする計画
D-最適化基準は、仮定したモデルに依存します。しかし、実際のモデルがどうなっているかは事前にはわからないため、D-最適計画のこの性質は弱点です。D-最適計画では、モデル係数の推定精度を最適化します。なお、極端なケースでは、D-最適計画の実験回数がパラメータと同数になり、あてはまりの悪さを確認するための自由度がない飽和モデルになってしまいます。
具体的には、D-最適計画は、行列式Dを最大化します。ここで、Dは次のように定義されます。
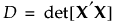
上の式で、Xは応答のシミュレートで定義されているようなモデル行列です。
D-最適分割計画は次のDを最大化します。
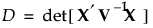
上の式で、V-1は応答の共分散行列で、ブロック対角行列になっています(Goos 2002)。
D-最適計画は、係数の標準誤差を最小化することに焦点を合わせているため、モデル自体が適切かどうかは検証されない傾向があります。たとえば、1次式モデルに対するD-最適計画には中心点は含まれません。仮定するモデルには含めないものの、実際には効果があるかも知れない項がある場合は、[可能な場合のみ]の項を指定してBayesのD-最適計画を用いる方が得策です。
Bayes流のD-最適化基準
Bayes流のD-最適化基準は、D-最適化基準を調整したもので、影響している可能性のある交互作用や非線形効果がある場合に役立ちます。DuMouchel and Jones(1994)およびJones et al(2008)を参照してください。
Bayes流のD-最適計画でも、「必ず推定したいパラメータ」を精度良く推定します。この「必ず推定したいパラメータ」に指定するには、「モデル」セクションにおいて「推定」を[必須]に設定します。Bayes流のD- 最適計画は、指定された実験サイズにおいて、それらの「必ず推定したいパラメータ」を精度良く推定すると同時に、その他の効果(特に、べき乗や交互作用などの高次の効果)もなるべく推定したい場合に用いてください。この「なるべく推定したい効果」に指定するには、「モデル」セクションにおいて「推定」を[可能な場合のみ]に設定します。Bayes流のD-最適計画は、限られた実験回数において、[必須]の効果しか含まないモデルの不適切さを検出することができます。
Bayes流のD-最適計画は、実験回数が、[必須]の項数より多く、かつ[必須]と[可能な場合のみ]の合計数より少ない場合に最も役立ちます。そのような場合には、すべての推定したいパラメータの個数より実験回数が少なくなっています。しかし、Bayes流の事前情報を加味して、すべての[必須]項を精度良く推定し、さらに[可能な場合のみ]の項の一部を検出・推定できるような計画が作成されます。
モデルパラメータに意味のある事前分布を適用するため、最適化基準の計算において、応答と因子が一定の性質を持つように尺度化されています(DuMouchel and Jones, 1994, Section 2.2)。
次の記号を用います。
• Xは、応答のシミュレートで定義されたモデル行列です。
• Kは、次のような値を持つ対角行列です。
– 推定が「必須」の項について、k = 0
– 推定が「可能な場合のみ」の効果で、かつ、主効果、べき乗の項、3水準以上のカテゴリカル因子が関係する交互作用について、k = 1
– その他の「可能な場合のみ」の項について、k = 4
[可能な場合のみ]のパラメータベクトルに対する事前分布は、平均が0で、共分散行列が対角行列であり、かつ、その対角要素が1/k2である多変量正規分布です。ここで、k2は、対応するパラメータの事前分散の逆数になっています。
kのデフォルト値は、経験則によって決められています。[可能な場合のみ]の主効果、べき乗、自由度が1より大きい交互作用の事前分散は1です。その他の[可能な場合のみ]項の事前分散は1/16です。なお、DuMouchel and Jones(1994)における記法では、k = 1/tが使われています。
[可能な場合のみ]の項の重みを制御するには、赤い三角ボタンのメニューから[詳細オプション]>[事前パラメータ分散]を選択します。[詳細オプション]>[事前パラメータ分散]を参照してください。
パラメータの事後分布の共分散行列は、(X′X + K2)-1です。Bayes流のD-最適計画は、次式で計算される、事後分布の共分散行列に対する逆行列の行列式を最大化することによって得られます。
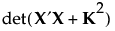
I-最適化基準
I-最適計画は、予測値の分散をデータ領域全体において平均した値を最小化します。実験の目的が係数(モデルパラメータ)を推定することではなく、以下のようなものであるような場合には、D-最適化基準よりI-最適化基準の方が適切です。
• 応答を予測する
• 応答が最適となる因子設定を特定する
• 応答が許容範囲内に収まるような計画領域を特定する
以上のようなケースでは、パラメータの推定精度より、応答の予測精度の方が重要です。
計画領域内の点x0における、未知の誤差分散に対する予測分散は、次のように計算します。
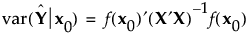
上の式で、Xは応答のシミュレートで定義されているようなモデル行列です。
I-最適計画は、計画領域全体の予測分散の積分Iを最小化します。Iは、次のように求められます。
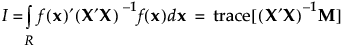
上の式で、Mはモーメント行列です。
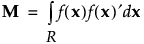
応答のシミュレートを参照してください。
モーメント行列は、計画に依存せず、事前に計算できます。行ベクトルf(x)′は、1と、仮定したモデルに該当する効果から成ります。たとえば、2つの連続尺度の因子の2次モデルf(x)′は、次のように定義されます。
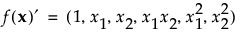
A-最適化基準
特定のモデル効果を強調したいときは、A-最適化基準を使用します。A-最適化基準を使うと、モデルのパラメータに重みを割り当てることができます。A-最適化基準は、それらの重みに基づいて計画を選択します。結果として生成される計画では、重みの大きい項の推定値の方が重みの小さい項の推定値より分散が小さくなるような因子の組み合わせが強調されます。たとえば、推定において、ある交互作用のグループが他の交互作用より重要だとします。重要な交互作用の重みを大きくすると、その推定値の分散が、他の交互作用に比べて小さくなります。
A-最適化基準は、モデル係数に対する推定値の共分散行列のトレースを最小化します。トレースとは、行列における対角要素の和です。A-最適計画は、回帰係数の分散の和を最小にする計画です。
Bayes流のI-最適化基準
BayesのI-最適計画は、[必須]の項と[可能な場合のみ]の項の計画領域全体における予測分散の平均を最小化します。
次の記号を用います。
• Xは、応答のシミュレートで定義されたモデル行列です。
• Kは、次のような値を持つ対角行列です。
– 推定が「必須」の項について、k = 0
– 推定が「可能な場合のみ」の効果で、かつ、主効果、べき乗の項、3水準以上のカテゴリカル因子が関係する交互作用について、k = 1
– その他の「可能な場合のみ」の項について、k = 4
[可能な場合のみ]のパラメータベクトルに対する事前分布は、平均が0で、共分散行列が対角行列であり、かつ、その対角要素が1/k2である多変量正規分布です。(kの値についての詳細は、Bayes流のD-最適化基準を参照してください。)
x0における予測値の事後分散は、次の式で計算されます。
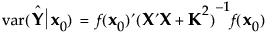
Bayes流のI-最適計画は、次式で表される、計画領域全体での予測分散の積分を最小化します。
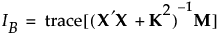
上の式で、Mはモーメント行列です。応答のシミュレートを参照してください。
交絡最適化基準
交絡最適化(alias optimality)は、仮定したモデルの効果と、モデルには含めていないものの影響している可能性のある効果との間にある交絡(別名関係; aliasing)を最小化します。後者の効果(モデルには含まれていないが影響している可能性のある効果)は、交絡項と呼ばれています。交絡最適計画の詳細は、Jones and Nachtsheim(2011b)を参照してください。
ここで、仮定したモデルの項に対応するモデル行列をX1とします(応答のシミュレートを参照)。交絡最適計画は、交絡項に対応するモデルも考慮します。交絡項のモデル行列をX2とします。
交絡行列(alias matrix)は、次のような行列Aで定義されます。
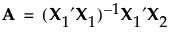
交絡行列の各要素は、モデル項の推定値におけるバイアス(偏り)にどの程度影響するかを示します。交絡行列の導出については、交絡行列を参照してください。
行列Aの要素の平方和は、バイアスに与える影響の全体的な大きさを表します。この平方和は、次のようなトレース(対角和)で表されます。
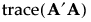
このトレースだけを最小化すると、一般に、D-最適計画よりD-効率が低くなってしまいます。そこで、交絡最適計画では、D-効率がある一定以上の値になるもののなかで、A′Aのトレースを最小化します。D-最適化基準の定義については、最適化基準を参照してください。交絡最適化におけるD-効率の下限値は、[詳細オプション]で指定されるD-効率の重みによって決まります。[詳細オプション]>[D効率の重み]を参照してください。