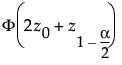ブートストラップの統計的詳細
この節では、ブートストラップの統計的詳細について説明します。
「小数の重み」の統計的詳細
この節では、ブートストラップ分析における小数の重みの計算方法を解説します。[小数の重み]オプションをオンにした場合は、ベイズ流のブートストラップ(Bayesian bootstrap; Rubin 1981)が実行されます。ある1つのブートスト ラップ標本において、同じデータ行が重複して抽出される回数を、「ブートストラップの重み」と呼びます。通常のブートストラップ法では、各ブートストラップの重みは、単純な復元抽出法によって決められます。
ベイズ流のブートストラップ法では、ブートストラップ抽出における抽出確率を確率変数とみなし、無情報の事前分布を仮定して、その事後分布を求めます。そして、抽出確率の乱数を、その事後分布から生成します。その抽出確率から、ブートストラップの重みを求めます。具体的には、以下の手順に従います。
• 形状パラメータが(n - 1)/n、尺度パラメータが1である、独立なガンマ分布に従うn個の乱数を生成する。
メモ: Rubin(1981)は、ガンマ分布の形状パラメータとして1を使用しています。JMPで採用している形状パラメータは、重みの平均と分散が、単純なブートストラップの重みの平均と分散に等しくなるように設定されています。
• S(n個の乱数の和)を計算する。
• n個の乱数のそれぞれにN/Sを掛けたものを、小数の重みとする(Nは行数、または、度数変数が指定されている場合は度数の合計)。
メモ: 分析において度数変数を使用した場合には、行ごとに、ガンマ分布の形状パラメータに、度数を掛け合わせます。ただし、度数の合計は、1より大きくなっているものとします。すると、形状パラメータはfi(N - 1)/Nに等しくなります(ここで、fiはi番目の行の度数の値、Nは度数の値の合計です)。
この手順で計算された各行の小数の重みは、その平均と分散が、単純なブートストラップの重みの平均と分散と等しくなっています。また、この手順で計算された各行の小数の重みは、正の値であり、すべてを合計するとN、その平均は1となっています。
バイアス修正済みの信頼限界の統計的詳細
この節では、バイアス修正済み(bias-corrected)のブートストラップ信頼限界(以下、「BC信頼限界」と述べます)について説明します。BC信頼限界は、結果のデータテーブルで「一変量の分布」スクリプトを実行すると、「ブートストラップ信頼限界」レポートに示されます。BC信頼限界は、ブートストラップ分布の非対称性に対処して、分位点の信頼限界を補正しています。Efron(1981)を参照してください。
表記
• p*は、ブートストラップ標本の推定値が、元の推定値以下となっている割合。
• z0は、標準正規分布のp*分位点。
• zαは、標準正規分布のa分位点。
BC信頼限界の両端
信頼水準が(1 - a)であるBC信頼限界は、ブートストラップ分布における以下の分位点です。
• 下限は、次の累積確率に対する分位点。
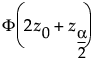
• 上限は、次の累積確率に対する分位点。