正準相関の計算に関する統計的詳細
ここでは、「モデルのあてはめ」プラットフォームの［MANOVA］手法で使用される正準相関の計算方法について説明します。
検定の詳細オプションの詳細
与えられた検定の［検定の詳細］オプションを選択すると、固有値、正準相関、固有ベクトルがレポートに表示されます。
［検定の詳細］オプションにより作成された正準相関は次のように計算されます。
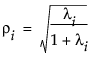
ここで、liは、多変量検定の統計値の計算に使用されるE-1H行列のi番目の固有値です。
「固有ベクトル」に表示されている行列はV行列です。これは、与えられた検定のE-1Hの固有ベクトルの行列です。
メモ: 与えられた検定のEおよびH行列には、元のEおよびH行列ではなくて、変換したM′EMとM′HMが使われます。M行列は、応答に対する計画行列です。この節で述べられているEおよびHは、多変量検定の統計的詳細で定義されています。
重心プロットオプションの詳細
全体および効果の重心は、次のように計算されます。
重心 =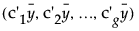 
効果j =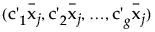 
ここで、
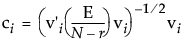
Nは、標本サイズ
viは、与えられた検定のE-1Hから求められた固有ベクトル行列Vの第i列
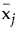は、j番目の効果に対する多変量の最小2乗平均
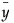は、応答値の全体平均
gは、E-1Hの固有値のうち、0より大きいものの個数
rは、X行列のランク
メモ: 与えられた検定のEおよびH行列には、元のEおよびH行列ではなくて、変換したM′EMとM′HMが使われます。M行列は、応答に対する計画行列です。この節で述べられているEおよびHは、多変量検定の統計的詳細で定義されています。
効果の重心半径は、次のように計算されます。
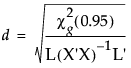
この式で、gは、E-1Hの固有値のうち0より大きいものの個数です。また、分母のLは、多変量の最小2乗平均を求めるのに使われた行列です。
［正準スコアの保存］オプションの詳細
Y値の正準スコアは、次のように計算されます。
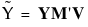
ここで、
Yは、応答変数の行列
M′は、応答変数に対する計画行列の転置行列
Vは、与えられた検定に対するE-1H固有ベクトルの行列
メモ: 与えられた検定のEおよびH行列には、元のEおよびH行列ではなくて、変換したM′EMとM′HMが使われます。M行列は、応答に対する計画行列です。この節で述べられているEおよびHは、多変量検定の統計的詳細で定義されています。
Y値の正準スコアは、0より大きい固有値に対応する固有ベクトルに対して保存されます。