競合原因分析の統計的詳細
競合原因分析モデルでは、全体の累積分布関数が次のように定義されます。
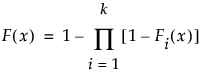
ここで、Fi(x), i = 1, …, kは、個々の原因における累積分布関数です。信頼限界も簡単に計算できます。関係する推定値がすべて最尤推定値だからです。
競合原因分析でのパラメータ指定
競合原因分析で、ある故障原因の分布パラメータを特定の値に固定したい場合は、その故障原因の「原因ごとの分析」レポートにてパラメータ値を指定します。「寿命の一変量 - 故障原因: <名前>」レポートにおける「パラメトリック推定」レポートでパラメータ値を指定してください。［モデルの更新］をクリックすると、指定したパラメータ値が設定され、全体の分布に反映されます。
この例では、競合原因分析でパラメータを指定する方法を説明しています。
1. ［ヘルプ］>［サンプルデータフォルダ］を選択し、「Reliability」フォルダにある「Appliance.jmp」を開きます。
2. ［分析］>［信頼性/生存時間分析］>［寿命の一変量］を選びます。
3. 「故障までの時間」を［Y, イベントまでの時間］に指定します。
4. 「原因コード」を［故障原因］に指定します。
5. 「信頼区間の方法」を［尤度］にします。
6. ［パラメータ指定の分布も使用する］を選択します。
7. ［OK］をクリックします。
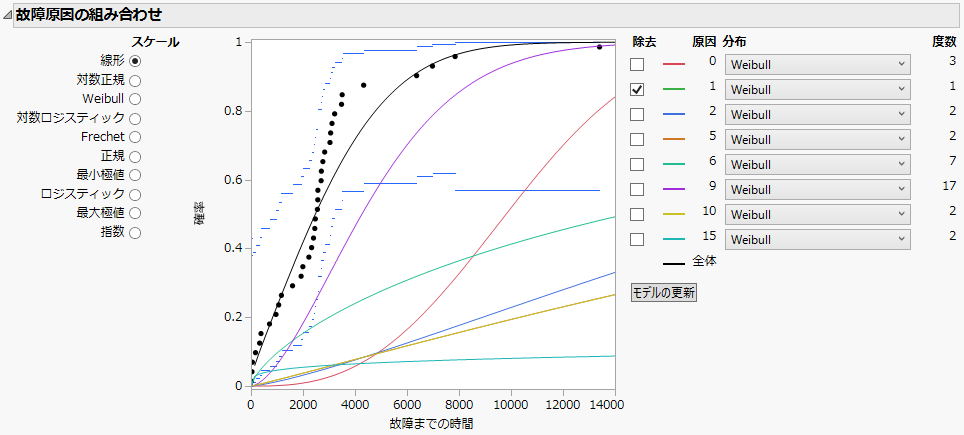
図3.25 原因1を削除したパラメータ指定モデル
デフォルトでは、原因1にはデータが十分ないので、「除去」されています。ここでは、この原因を「除去」として処理したくないとします。
8. 原因1の「原因ごとの分析」レポートを開きます。「寿命の一変量 - 故障原因:1 度数：1」という名前のレポートです。
9. 「パラメトリック推定 - Weibull」の赤い三角ボタンをクリックし、［分布パラメータの指定］を選択します。
10. ［Weibull β］を選択して、「2」を入力します。
11. ［更新］をクリックします。
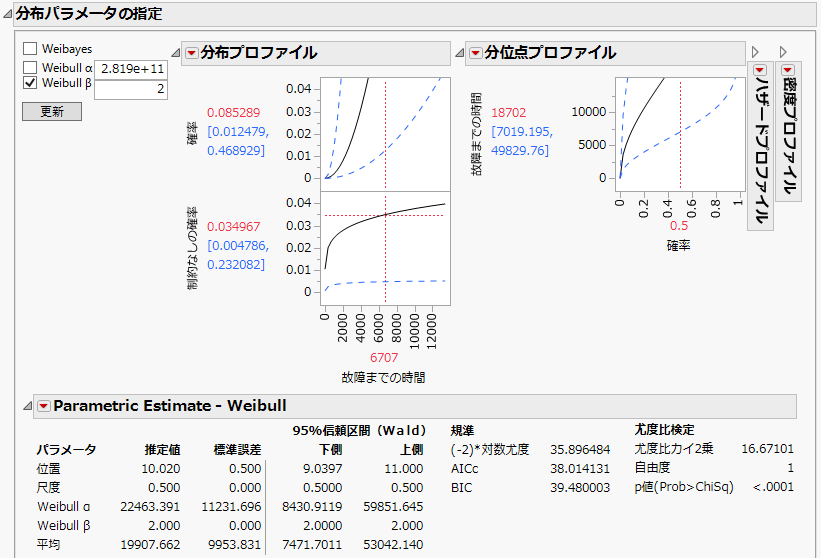
図3.26 Weibull βを指定したパラメータ指定モデル
「パラメトリック推定値 - Weibull」レポートで、bを2と仮定すると、パラメータαは22463.391と推定されます。以下の操作により、この分布を原因1の故障分布に使用します。
12. レポートウィンドウの最上部の「故障原因の組み合わせ」が表示されるまで上にスクロールします。
13. 原因1の「除去」ボタンを選択解除します。
14. 原因1の分布に、［パラメータ指定 Weibull］を選択します。
15. ［モデルの更新］をクリックします。
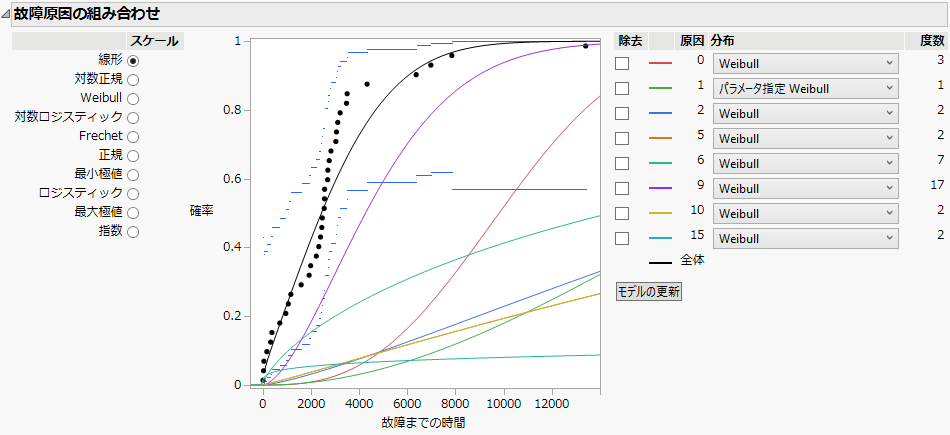
図3.27 原因1が表示された更新モデル
これらの操作により、パラメータが指定されたWeibull分布を原因1に適用して、全体のモデルが計算されました。
競合原因分析でのBayes推定
故障原因にBayesモデルを指定するには、競合原因分析でのパラメータ指定の手順と同じような手順に従います。各原因に対する「寿命の一変量」の「統計量」の「パラメトリック推定」における「Bayes推定」レポートで、Bayesモデルを指定します。Bayes推定 - <分布の名前>を参照してください。
ある原因に対してBayes推定が適用された場合、全体の累積分布関数を求めるのに乱数シミュレーションが利用されます。たとえば、2つの故障原因があるとします。1つ目の原因には通常のWeibull分布を最尤推定し、2つ目の原因ではWeibull分布をBayes推定したものを用いるとします。このとき、1つ目の原因においては、パラメータベクトルq1を推定するのに最尤法が使われます。一方、2つ目の原因においては、パラメータベクトルq2の事後分布を求めるのにBayes推定が使われます。
この場合、全体における累積分布関数F(x, q1, q2)の事後分布での分位点や中央値は、次のように求められます。
• 1つ目の原因に対してはパラメトリックなブートストラップを実行します。最尤推定値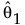
の漸近分布から標本を乱数で生成します。
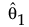に対する漸近分布から生成された値を
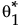とします。
• 一方、2つ目の原因に対しては、Bayes推定の枠組みで、q2の事後分布に従う乱数を生成します。これを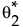
とします。
• 生成された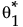
と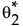
の各セットに対して、F(x, q1, q2)に対する推定値F*(x, q1, q2)を求めます。
• F*(x, q1, q2)から、全体の累積分布関数における中央値や分位点を求めます。これらの中央値や分位点が、分布プロファイルにおいて、対応するx値のところにプロットされます。
競合原因分析でのWeibayes分析
故障原因にWeibayesモデルを指定する手順は、競合原因分析でのパラメータ指定の手順と同様です。まず、各原因に対する「寿命の一変量」の「統計量」の「パラメトリック推定 - Weibull」レポートで、［分布パラメータの指定］を選択してください。そして、「分布パラメータの指定」レポートで、「Weibayes」オプションにチェックを入れてください。競合原因分析においてはWeibayesモデルがBayesモデルとして処理され、パラメータαの事後分布からブートストラップ標本が抽出されます。Liu and Wang（2013）を参照してください。
競合原因分析での平均余寿命の計算
競合原因分析での平均余寿命は、故障時間を乱数シミュレーションで生成することにより計算されています。「平均余寿命の計算」の赤い三角ボタンのメニューの［設定］オプションにより生成される乱数の個数を変更できます。この乱数の個数を、ここではmとします。
時間tでの平均余寿命の推定値を求めるために、「時間tまで生存していたもの」という条件付けをした分布からm個の乱数を生成します。そして、これらの乱数の平均を計算します。
平均余寿命に対する信頼区間をJMPに計算させるには、「設定」ウィンドウのチェックボックスを選択する必要があります。そのチェックボックスにチェックすると、ブートストラップ標本の回数（ブートストラップ標本の標本数）を設定するためのオプションが表示されます。この回数をnとします。
信頼区間を計算するために、最尤推定値の漸近分布、またはBayes推定における事後分布のどちらかに基づいて、シミュレーションがn回、行われます。1回のシミュレーションごとにm個の乱数が生成され、そのm個の乱数から平均余寿命が計算されます。そして、n個の平均余寿命から、信頼区間が計算されます。
［混合分布のあてはめ］での予測式の保存
ここでは、「混合分布」レポートの［予測の保存］オプションによって保存される式を説明します。
次の記号を用います。
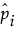は、混合の割合wiに対する推定値です。
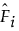は、累積分布関数Fiに対する推定値です。
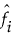は、Fiに対応した確率密度関数に対する推定値です。
• 観測値yが打ち切りデータではない場合、保存される値は次のように求められます。
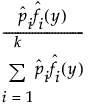
• 観測値が打ち切りデータの場合には、打ち切りがなかった場合における上式の確率密度値を、以下に述べるものに置き換えて求められます。
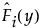（右側打ち切りの場合）
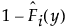（左側打ち切りの場合）
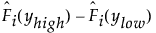（区間打ち切りの場合）