推定法の統計的詳細
「モデルのあてはめ」プラットフォームの［一般化回帰］手法の推定法には、罰則付き回帰が含まれます。この手法では、回帰係数に罰則を課すことによって、推定にバイアス（偏り）が生じます。
リッジ回帰
リッジ回帰では、回帰係数にl2ペナルティが適用されます。この係数の推定値は、次のように定義されます。
、
この式で、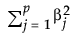
はl2ペナルティ。lは調整パラメータ、Nは行数、pは変数の数です。
Dantzig選択器
Dantzig選択器では、目的関数として残差とX列の内積のl∞ノルムが使われます。Dantzig選択器の推定値は、次のように求められます。
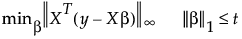
この式で、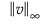
はl∞ノルムを表します。このノルムは、vベクトルにおける要素の絶対値のうち最大のものです。
Lasso回帰
Lasso回帰では、回帰係数にl1ペナルティが適用されます。この係数の推定値は、次のように定義されます。
、
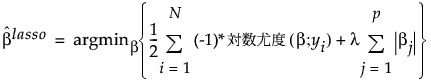この式で、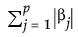
はl1ペナルティ。lは調整パラメータ、Nは行数、pは変数の数です。
弾性ネット
弾性ネットは、l1とl2の両ペナルティを組み合わせて使用します。弾性ネットの係数の推定値は、次のように定義されます。
、
この式で使われている記号は次のとおりです。
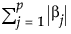は、l1ペナルティ
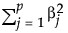は、l2ペナルティ
lは、調整パラメータ
aは、l1ペナルティとl2ペナルティの配分を決定するパラメータ
Nは、標本サイズ
pは、変数の個数
ヒント: 説明変数が1つしかない弾性ネットモデルで、aとlを変化させたときの縮小効果を示す2つのサンプルスクリプトがあります。［ヘルプ］>［サンプルの索引］を選択し、［サンプルスクリプトディレクトリを開く］をクリックして、［demoElasticNetAlphaLambda.jsl］または［demoElasticNetAlphaLambda2.jsl］を選択してください。それぞれのスクリプトの先頭に、使用法と表示される内容説明が（英語で）記載されています。
適応型手法
適応型Lassoの手法では、重み付きのペナルティを使って、一致推定値を求めます。重み付きのl1ペナルティの計算式は次のとおりです。
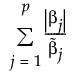
この式で、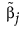
は、最尤推定値が存在する場合は最尤推定値です。応答変数の確率分布として正規分布を指定したときで、最尤推定値が存在しない場合には、
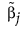には一般化逆行列を使って求めた最小2乗推定解が使われます。応答変数の確率分布として正規分布以外のものを指定したときで、最尤推定値が存在しない場合には、
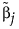にはリッジ回帰の解が使われます。
適応型Lassoの場合、この重み付きl1ペナルティを使って、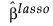
係数が決定されます。
適応型弾性ネットの場合は、この重み付きl1ペナルティを使い、さらにl2ペナルティにも重みを付けます。適応型弾性ネットの重み付きl2ペナルティの計算式は次のとおりです。
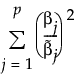
この式で、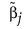
は、最尤推定値が存在する場合は最尤推定値です。応答変数の確率分布として正規分布を指定したときで、最尤推定値が存在しない場合には、
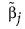には一般化逆行列を使って求めた最小2乗推定解が使われます。応答変数の確率分布として正規分布以外のものを指定したときで、最尤推定値が存在しない場合には、
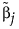にはリッジ回帰の解が使われます。