一般化回帰モデル

変数選択によってモデルを構築する

「モデルのあてはめ」プラットフォームの「一般化回帰」手法は、JMP Proのみで使用できます。

「一般化回帰」手法は、回帰分析の枠組みにおいて、パラメータ推定値を縮小（shrink; 収縮）させたり、変数選択を行ったりします。この手法は、相関の高い説明変数が多数あるようなデータで役立ちます。用意されている方法のうち、Lassoと弾性ネットは、パラメータ推定値を縮小させるとの同時に、変数選択も行います。

相関の高い説明変数が多数あるデータでは、一般的に、多重共線性の問題が生じます。最近のデータでは、標本サイズよりも変数の個数の方が多いこともあります。そのような場合は、変数を選択する必要があります。しかし、多重共線性や説明変数が多数あることにより、従来の方法ではうまく分析できないことがあります。

実験計画で得られたデータなどの、小規模で相関があまりないようなデータでも、Lassoや弾性ネットは役立ちます。予測モデルを作成する場合や、モデルに含める変数を選択する場合にこれらの方法は役立ちます。

「一般化回帰」手法は、さまざまなモデルをサポートしています。「一般化回帰」手法では、応答変数の分布として、さまざまな分布を用意しています。たとえば、正規分布（応答が連続尺度のとき）、二項分布やPoisson分布（応答が度数のとき）、ゼロ強調（zero inflated）の分布が用意されています。「一般化回帰」は、説明変数を取捨選択したい場合や、説明変数に共線性がある場合に役立ちます。また、これらのモデルを、最尤法に基づく従来のモデルと比較するのにも使えます。

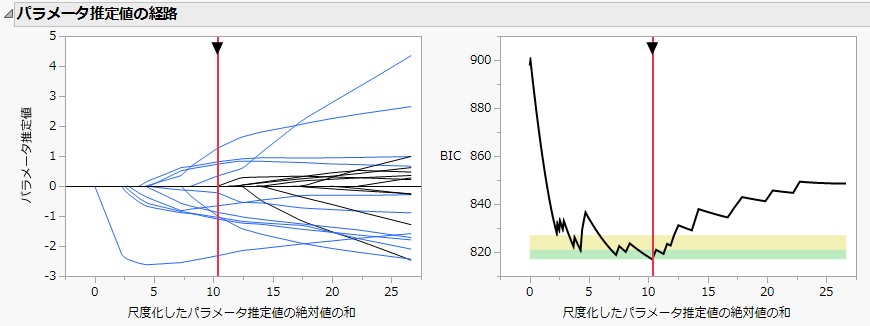
図6.1 弾性ネットのパラメータ推定値の経路 

目次

一般化回帰手法の概要

一般化回帰の例

「一般化回帰」手法の起動

分布の指定

「一般化回帰」レポートウィンドウ

「一般化回帰」レポートのオプション

「モデルの設定」パネル

応答変数の分布

「推定法」のオプション

詳細設定

「検証法」のオプション

早期打ち切り

実行

モデルのあてはめ結果に関するレポート

回帰プロット

モデルの要約

推定値の詳細

パラメータ推定値の経路

標準化した説明変数に対する推定値

元の説明変数に対する推定値

非ゼロの推定値

効果の検定

あてはめたモデルに対するオプション

SVEM（Self-Validated Ensemble Models）

SVEMの概要

SVEMのレポート

SVEM法で得られた結果に対するオプション

一般化回帰手法の統計的詳細

推定法の統計的詳細

「詳細設定」の統計的詳細

分布の統計的詳細

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).