外挿の抑制指標の統計的詳細
予測プロファイルの［外挿の抑制］オプションでは、以下に述べる2つの指標のいずれかによって、点が外挿であるかどうかが判断されます。分析の種類によって、2つの指標のいずれが使われるかが異なります。
てこ比
「モデルのあてはめ」プラットフォームの［標準最小2乗］手法では、てこ比が外挿の指標として使用されます。
i番目の観測のてこ比hiiは、X(X′X)-1X′という行列のi番目の対角要素（ハット値）です。新しい予測点のてこ比は、次の式で計算されます: hpred = x′pred(X′X)-1xpred。 てこ比がhpredである予測が外挿かどうかを判断するために、次の2つの基準を使用できます。
• hpred > K × max(hii)。ここで、Kは、分析者が指定する乗数です
• hpred > L × p/n。ここで、Lは分析者が指定する乗数、pは変数の個数、nは観測数、p/nは平均てこ比です
「閾値の基準を設定」オプションを使用して、使用する基準および乗数の値を指定できます。乗数のデフォルト値は、K = 1およびL = 3です。
メモ: 保存された最小2乗法モデルを使用して［グラフ］メニューからプロファイルに対する外挿の抑制を実行する場合、てこ比の方法は使用されません。代わりに、正則化されたHotellingのT2方法が使用されます。
正則化されたHotellingのT2
最小2乗法以外のモデルでは、正則化されたHotellingのT2の値が外挿指標として使用されます。学習データのT2値と予測点のT2値は、次のように計算されます。
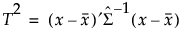
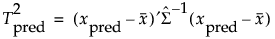
ここで、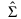
は、学習データから推定された、Schafer and Strimmerの正則化共分散行列です。ここでのSchafer-Strimmer正則化共分散行列の計算に使用される目標行列は、対角共分散行列です。Schafer and Strimmer（2005）を参照してください。欠測値のある行もモデルの学習に使われるプラットフォームでは、欠測値をペアワイズ法で処理して共分散行列は計算されます。
メモ: なお、カテゴリカル変数は指示変数に変換されます。
学習データでの、欠測値にならないT2の個数によって、以下のように閾値は計算されます。
• 欠測値でないT2が10個以上ある場合、閾値は次のように設定されます。
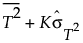
ここで、
Kは、分析者が指定する乗数。デフォルトは3
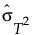はT2の標準偏差
• 欠測値でないT2が10個未満の場合、閾値はKsに相当する分位点が、F分布の分位点から計算されて、設定されます。
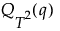
ここで、
q = F(K)
F(·)は標準正規分布
Kは、分析者が指定する乗数。デフォルトは3
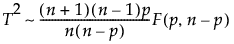
pは、パラメータの個数
nは、欠測値でないT2の個数