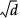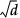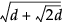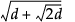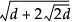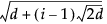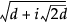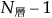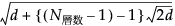シミュレータの統計的詳細
分布として[正規 加重]が選ばれた場合、多変量正規分布の中心からの距離で層別にした乱数生成法が使われます。この方法は、極端に大きな値や小さな値を考慮しなければいけない場合に、他の重点サンプリング法よりも良い結果をもたらすと考えられます。
最初に層数を定義します。各層は、0を中心とする、特定の区間を半径とする超球面になっています。d個の因子に対して、各層は半径を区間ごとに定義されています。Table 8.1を参照してください。
|
層の番号 |
内側の距離 |
外側の距離 |
|---|---|---|
|
0 |
0 |
|
|
1 |
|
|
|
2 |
|
|
|
i |
|
|
|
|
|
|
デフォルトの層数は16です。層数を変更する場合は、Shiftキーを押したまま[シミュレータ]の赤い三角ボタンをクリックすると、非表示のコマンド[層数]が表示されるので、それを選択します。標本サイズが層の数でちょうど割り切れない場合は、標本サイズをその分0だけ増やします。
1組の乱数を生成するのに次のような処理が行われます。
1. 第i個目の乱数生成に対する層としてmod(i - 1, N層数)を選択します。
2. n次元におけるランダムな方向を求めるために、n個の独立な正規分布に従う乱数を生成し、その大きさを1にします。
3. 一様分布の乱数を、該当している層に対応したカイ2乗分布の分位点に変換することにより、中心からの距離の乱数を生成します。
4. 大きさ1に基準化されたランダムな方向をもつベクトルを、その距離の大きさになるように尺度変換します。
5. 最後に、生成された乱数を各因子の平均と標準偏差に合わせて変換します。
できあがった乱数の分布は、正しく加重して推定すれば、指定された平均と標準偏差を持った多変量正規分布の乱数として使えます。「一変量の分布」プラットフォームにおいて、重みを使って標準偏差などを計算しても、適切な推定値が計算されないことに注意をしてください。ただし、重みに大きな値(たとえば1012)を掛け合わせ、それを[度数]として使えば、正しい標準偏差になります。