横長データに対する推定法の統計的詳細
ここでは、「主成分分析」起動ウィンドウで「計算方式」として[横長データ]を指定したときの推定法について詳しく説明します。この方法は、特異値分解に基づいており、共分散行列を計算しなくて済むため、計算処理が効率化されます。
完全特異値分解
完全特異値分解(full SVD)は、すべての次元の特異値および特異ベクトルを求めます。次の記号を用います。
• n = 行数(標本サイズ)
• p = 変数の個数
• X = データ値のn × p行列
0以外の固有値の個数は、求めることができる主成分の個数であり、Xの相関係数行列のランクと同じです。0以外の固有値の数は、nとpの小さい方を超えることはできません。
完全特異値分解を適用する前に、データを標準化しています。データの標準化とは、データから平均を引き、それを標準偏差で割る変換を指します。標準化したデータを、Xs(n × p行列)と記します。標準化していないデータXの相関係数行列は、標準化したデータの共分散行列です。よって、次のように相関係数行列は表されます。
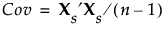
Xsは、特異値分解した行列によりUDiag(Λ)V′と表されます。この特異値分解により、固有ベクトルとXs′Xsの固有値が求められます。なお、主成分スコアはXsVによって求められます。詳細については、「線形 横長データ」の手法と特異値分解を参照してください。
 切り捨て特異値分解
切り捨て特異値分解
切り捨て特異値分解では、完全特異値分解とは異なり、特異値および特異ベクトルを指定された個数しか求めません。そのため、固有値と主成分に関しても指定された個数だけしか求めません。アルゴリズムの詳細については、Baglama and Reichel(2005)を参照してください。
乱択特異値分解
乱択特異値分解では、完全特異値分解とは異なり、低ランク行列近似を2段階に分けて行います。大まかにいうと、低ランク行列近似では、m × p行列Aを近似するために、A ≈ BCとなるようなm × k行列Bとk × p行列Cを求めます。ここで、kはpよりはるかに小さいものとします。
完全特異値分解と同じ記号を用いて、Xsを分解してみましょう。
乱択特異値分解の第1段階では、次のような行列Qを求めます。
• Qは、l個の正規直交列から構成される行列。ここで、k ≤ l ≤ pとします。
• Xs ≈ QQ′Xs
できるだけ列数が少ないQを効率的に計算する方法は、Halko, Martinsson, and Tropp(2011)で説明されています。
第2段階では、このQの転置行列をXsに掛けた行列を特異値分解します。その掛けて得られる行列をB = Q′Xsとすると、次が成り立ちます。
B = Q′Xs ⇒ QB = QQ′Xs ⇒ QB = Xs
このBは、Xsよりはるかに小さい行列となっているので、計算量が少なくてすみます。この行列に対する特異値分解から、次のようにして元の行列の特異値分解を求めます。
B ≈ U*Diag(Λ)V′
QB ≈ (QU*)Diag(Λ)V′
A ≈ UDiag(Λ)V′ ここでU = QU*
乱択特異値分解のアルゴリズムの詳細については、Halko, Martinsson, and Tropp(2011)を参照してください。