主成分分析

多変量データの次元削減

主成分分析（PCA; Principal Component Analysis）は、複数の変数における変動をできるだけ説明する、少数の独立した線形結合（主成分）を求めます。主成分分析は次元を削減する手法であり、探索的データ分析（EDA; Exploratory Data Analysis）の手法の1つです。主成分回帰（PCR; PCA regression）によって予測モデルを作成するときにも使えます。

「主成分分析」プラットフォームには、変数の個数が非常に多いデータに対する処理として、「横長データ」（wide）というオプションも用意されています。「横長データ」に対する手法では、横長なデータに対して、通常の処理方法よりも計算時間が短くてすみます。主成分スコアをデータテーブルに保存すれば、それをもとに主成分回帰が行えます。

多くの0があるデータ（疎データ）に対する処理も用意されています。疎データに対する処理も計算時間が短くなります。ただし、こちらの疎データに対する処理では、全次元の主成分は算出されず、主成分はユーザが指定した個数だけが算出されます。

また、因子分析を行うには、専用の「因子分析」プラットフォームがありますが、「主成分分析」プラットフォームでも因子分析を行うことができます。JMPの因子分析では、抽出した因子を解釈しやすくするために、いくつかの直交回転や斜交回転が用意されています。因子分析については、因子分析を参照してください。

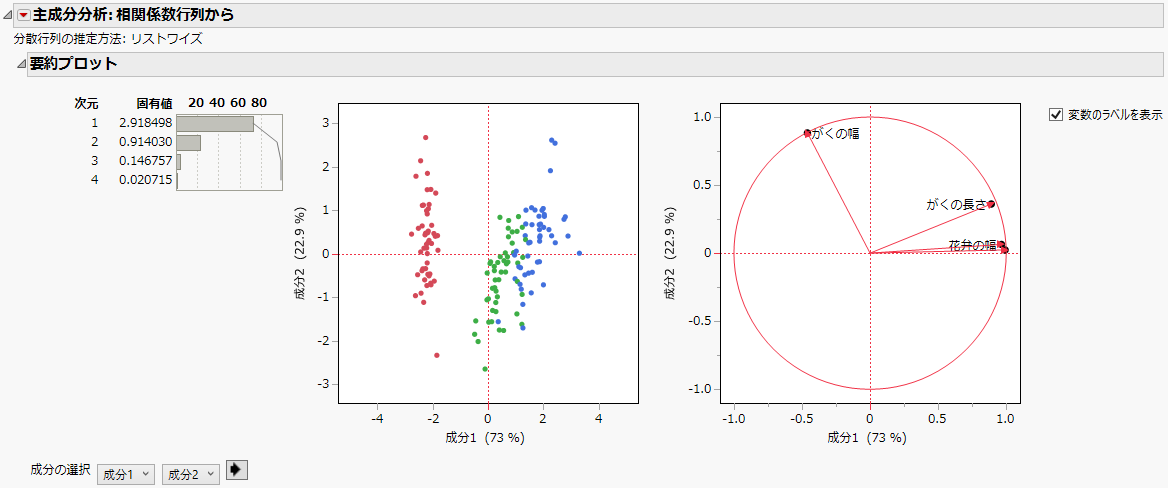
図4.1 主成分分析の例 

目次

「主成分分析」プラットフォームの概要

主成分分析の例

「主成分分析」プラットフォームの起動

欠測値のあるデータ

「主成分分析」レポート

「主成分分析」レポートのオプション

外れ値分析

「主成分分析」プラットフォームの統計的詳細

共分散行列の推定法に関する統計的詳細

横長データに対する推定法の統計的詳細

外れ値分析の計算の統計的詳細