拟合线、拟合多项式和特殊拟合报表

在“二元”平台中，使用“拟合线”、“拟合多项式”或“特殊拟合”选项拟合回归模型。您可以拟合多个模型，然后在散点图上比较这些拟合。

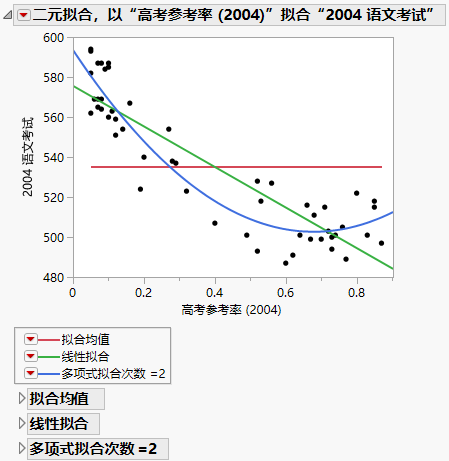
图 5.8 拟合线和拟合多项式的示例 

有关“线性拟合”和“多项式拟合次数”菜单中的选项的详细信息，请参见二元拟合选项。有关统计详细信息，请参见“拟合线”选项的统计详细信息。

在“二元”平台中，您选择的每个拟合都有一个报表。“线性”、“多项式”和“变换拟合”报表各自包含一个含有拟合方程的文本框。每个拟合报表都包含拟合汇总表、方差分析 (ANOVA) 表和参数估计表。若数据中存在重复，则会出现第四个表，即失拟表。变换 Y 变量的拟合包括原始尺度表上的拟合测度的汇总。

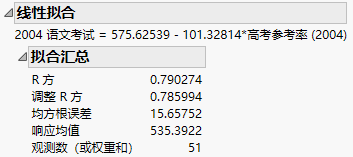
拟合汇总

在“二元”平台拟合报表中，“拟合汇总”表包含模型拟合的数值汇总。拟合方程显示在“拟合汇总”表的上方。

图 5.9 “拟合汇总”表 

“拟合汇总”表包含以下统计量：

R 方

模型解释的变异的比例。剩余变异由随机误差造成。若模型完全拟合，则 R 方为 1。请参见“拟合汇总”报表的统计详细信息。

注意：较低的 R 方值表明可能有一些模型中未包含的变量可以解释无法解释的变异。不过，若数据受大量的内在变异影响，即便是有用的回归模型也可能具有较低的 R 方值。阅读您的研究领域中的文献材料，了解有关典型 R 方值的信息。

调整 R 方

针对模型中的参数数目调整的 R 方统计量。调整 R 方有利于包含不同数目参数的模型间进行比较。请参见“拟合汇总”报表的统计详细信息。

均方根误差

随机误差标准差的估计。该数量是“方差分析”报表（图 5.11）中误差均方的平方根。

响应均值

响应变量的样本均值（算术平均值）。若未指定模型效应，则为预测响应。

观测数（或权重和）

用于估计拟合的观测数。若有权重变量，则为权重和。

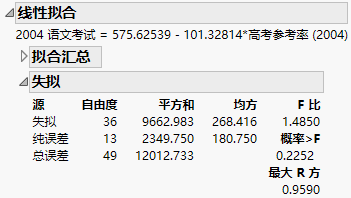
失拟

在“二元拟合”报表中，“失拟”表包含失拟检验的结果。仅当存在重复的 X 值且模型未饱和时，失拟检验才可用。根据重复值计算的平方和称为纯误差。这是总体误差中无论使用哪种形式的模型都无法解释或预测的部分。

图 5.10 线性拟合的“失拟”表 

模型剩余误差与纯误差之间的差值称为失拟误差。若模型指定有误，则失拟误差可能显著大于纯误差。指定有误的模型是未能很好描述数据的模型。失拟检验的原假设是失拟误差为 0。因此，较小的 p 值指示失拟显著。

“失拟”表包含以下列：

源

变异的三个来源：失拟、纯误差和总误差。

自由度

每种误差来源的自由度 (DF)。

‒ “总误差自由度”是对应的“方差分析”(ANOVA) 表的误差行中的自由度。请参见方差分析。“总误差自由度”值是 ANOVA 表中的“总自由度”值和“模型自由度”值之间的差值。误差自由度又分为失拟自由度和纯误差自由度。

‒ 纯误差自由度是每个重复观测组的合并结果。请参见“失拟”报表的统计详细信息。

‒ 失拟自由度是总误差自由度与纯误差自由度之间的差值。

平方和

每种误差来源的平方和 (SS)。

‒ 总误差平方和是相应的“方差分析”表的误差行中的平方和。请参见方差分析。

‒ 纯误差 SS 是每个重复观测组的合并结果。用纯误差平方和除以其自由度可估计给定的预测变量设置下的响应方差。该估计值不受模型影响。请参见“失拟”报表的统计详细信息。

‒ 失拟平方和是总误差平方和与纯误差平方和之间的差值。若失拟平方和较大，则模型可能不适用于数据。

均方

源的均方，它是平方和除以自由度的结果。与纯误差均方相比，较大的失拟均方表明模型拟合不佳。F 比可用于进行正式的假设检验。

F 比

失拟均方与纯误差均方之比。F 比的值越大，失拟误差为 0 的可能性就越小。

概率 > F

失拟检验的 p 值。原假设为失拟误差为 0。较小的 p 值指示失拟显著。

最大 R 方

某个模型仅使用该模型所含变量可以实现的最大 R2 值。请参见“失拟”报表的统计详细信息。

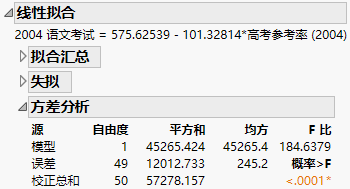
方差分析

在“二元拟合”报表中，“方差分析”表包含用于将拟合模型与所有预测值都等于响应均值的模型进行比较的计算。方差分析 (ANOVA) 表中的值用于计算 F 比来评估模型的有效性。若与 F 比关联的 p 值较小，则认为相对于只有响应均值的模型是更适合数据的拟合。

图 5.11 线性拟合的“方差分析”表 

“方差分析”表包含以下列：

源

变异的三个来源：模型、误差和校正总和。

自由度

每个变异来源关联的自由度 (DF)。校正总和自由度始终为观测数减 1，它按以下方式分为模型自由度和误差自由度：

‒ 模型自由度是用于拟合模型的参数数目（截距除外）。

‒ 误差自由度是校正总和自由度与模型自由度之间的差值。

平方和

每个变异来源关联的平方和 (SS)：

‒ 总（校正总和）平方和是响应值与样本均值之间的差值平方和。它表示响应值中的总变异。

‒ 误差平方和是拟合值与实际值之间的差值平方和。它表示拟合模型尚未解释的变异。

‒ 模型平方和是校正总和平方和与误差平方和之间的差值。它表示模型解释的变异。

均方

变异的模型和误差源的均方统计量。每个均方值都是平方和除以其相应自由度的结果。

注意：误差均方的平方根与“拟合汇总”表中的 RMSE 相同。

F 比

模型均方除以误差均方。F 比是以下检验的检验统计量：检验模型是否与所有预测值都是响应均值的模型显著不同。该拟合的假设前提是所有回归参数（截距除外）都为零。若该假设成立，则误差均方和模型均方都估计误差方差，并且它们的比值服从 F 分布。

概率 > F

观测到的检验的显著性概率 (p) 值。较小的 p 值被视为回归效应的证明。

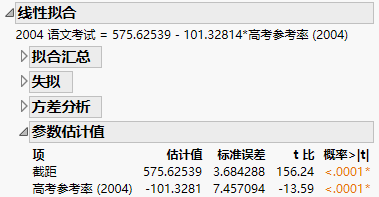
参数估计值

在“二元拟合”报表中，“参数估计值”表包含模型参数估计值。

图 5.12 线性拟合的“参数估计值”表 

“参数估计值”表包含以下列：

项

与估计参数对应的模型项。第一个项是截距。

估计值

每个项的参数估计值。这些值是模型系数的估计值。

标准误差

参数估计值的标准误差估计值。

t 比

假设每个参数为零的检验统计量。这是参数估计值与其标准误差的比值。在有关模型的一般假设下，t 比服从 Student t 分布。

概率>|t|

实际参数值为零（而不是双侧备择假设下它不为零）的检验的 p 值。

要显示其他统计量，请在报表中右击并选择列菜单。默认情况下不显示以下统计量：

95% 下限

参数估计值的 95% 置信下限。

95% 上限

参数估计值的 95% 置信上限。

标准 Beta

回归模型的参数估计值，模型中所有项都标准化为均值等于 0 且标准差等于 1。请参见“参数估计值”报表的统计详细信息。

VIF

显示模型中每个项的方差膨胀因子 (VIF)。高 VIF 值指示模型中的项存在共线性问题。

设计标准误差

参数估计值的相对方差的平方根。请参见“参数估计值”报表的统计详细信息。

基于原始尺度衡量的拟合

在“二元拟合”报表中，“基于原始尺度衡量的拟合”表包含采用未变换尺度衡量的模型拟合的数值汇总。仅当 Y 变量已变换时，该表才可用。