启动“主成分”平台

通过选择分析 > 多元方法 > 主成分来启动“主成分”平台。“多元”平台和“三维散点图”平台也提供主成分分析。

主成分分析的示例中所述的示例使用 Solubility.jmp 样本数据表中的所有连续变量。

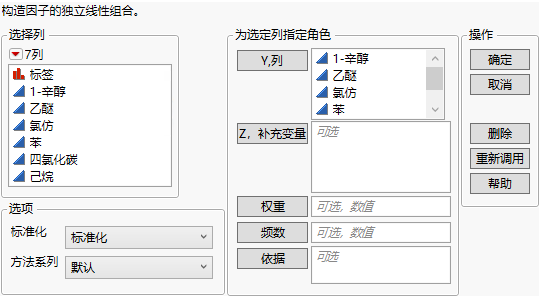
图 4.3 “主成分”启动窗口 

有关“选择列”红色小三角菜单中选项的详细信息，请参见《使用 JMP》中的““列过滤器”菜单”。

Y，列

要进行成分分析的变量。

Z，补充变量

要显示的补充变量。补充变量不包含在主成分计算中，包括它们不会影响结果。连续型补充变量可以投影到载荷图中，用于增强解释。

权重

标识一列，该列的数值为分析中的每一行都分配一个权重。

注意：“宽”方差估计方法和“稀疏”方差估计方法忽略“权重”角色。

频数

标识一列，该列的数值为分析中的每一行都分配一个频数。

注意：“宽”方差估计方法和“稀疏”方差估计方法忽略“频数”角色。

依据

为“依据”列指定的每个值创建“主成分”报表，以便您可以为每个组执行单独的分析。

标准化

指定每列是否中心化和标准化。这决定了用于计算主成分的矩阵。

标准化

分别对每列执行中心化和标准化。基于相关性矩阵计算主成分。

未统一尺度

分别对每列执行中心化。基于协方差矩阵计算主成分。

未统一尺度且未中心化

基于未统一尺度且未中心化的矩阵计算主成分。

方法系列

指定数据类型。

默认

若列数小于 500 或小于行数，则将“窄数据”指定为“方法系列”。若列数大于 500 并且大于行数，则 JMP 警示窗口会推荐宽估计方法。点击宽方法（快速）以使用宽数据估计方法，或点击默认方法（慢速）以使用窄数据估计方法。

窄数据

使用协方差矩阵、相关性矩阵或未统一尺度且未中心化的矩阵获取主成分。

宽数据

使用奇异值分解获取主成分。

方差估计

（仅当将“窄数据”指定为“方法系列”时才可用。）指定计算相关性的方法。其中有些方法解决了缺失数据的处理。

默认

默认选项使用“逐行”、“配对”或“REML”方法。“JMP 警示”还建议在适当的时候切换至“宽”方法。

• 逐行估计用于不含缺失值的数据表。

• 配对估计用于包含缺失值并且多于 10 列、多于 5,000 行或列数多于行数的数据表。

• 在其他情况下使用 REML 估计。

REML

限制最大似然 (REML) 估计使用所有数据，即使存在缺失值。由于存在偏倚修正因子，若您的数据集很大且包含许多缺失值，该方法会很慢。因此，REML 最适用于较小的数据集。若数据中不含缺失单元格，则 REML 和 ML 估计值等价于样本协方差矩阵。若存在缺失单元格，与 ML 估计相比，REML 的方差和协方差估计值的偏倚更小。有关统计详细信息，请参见REML。

ML

最大似然 (ML) 估计使用所有数据，即使存在缺失值。由于 ML 的估计值生成速度更快，该方法最适用于包含缺失数据的大数据表。

稳健

稳健估计使用所有数据，即使存在缺失值。该方法降低了极值的权重，因此最适用于可能具有离群值的数据表。有关统计详细信息，请参见“稳健”。

逐行

逐行估计为每对列计算 Pearson 相关性系数。有关统计详细信息，请参见“Pearson 乘积矩相关系数的统计详细信息”。逐行估计不使用包含缺失值的观测。该方法可用于排除包含缺失数据的所有观测。

配对

配对估计使用所有数据，即使存在缺失值。该方差估计方法使用这两列中不含缺失值的所有观测为每对列计算 Pearson 相关性系数。有关统计详细信息，请参见“Pearson 乘积矩相关系数的统计详细信息”。配对估计最适用于包含缺失值并且列数多于行数、多于 10 列或多于 5,000 行的数据表。

• 若您选择“REML”、“ML”或“稳健”，而您的数据表中的列数多于行数并且具有缺失值，JMP 会将“方差估计”切换为“配对”。

• 若您选择“稳健”而您的数据表中的列数多于行数并且不含缺失值，则 JMP 会将“方差估计”切换为“逐行”。

• 若数据表超过 500 列且列数多于行数，则无论最初选择哪种方法，JMP 都会将“方差估计”切换为“宽”。

注意：对于数据表超过 500 列并且列数多于行数的情况，“JMP 警示”窗口会建议使用宽估计方法。这是因为在列数过多时使用其他方法，计算时间会相当长。点击宽方法（快速）以切换为宽估计方法，或点击默认方法（慢速）以使用您最初选定的方法。

成分数

（仅当将“宽数据”指定为“方法系列”时才可用。）指定要估计的成分数。通常，成分数远小于数据的维。

指定

使用“截断 SVD”估计方法估计指定数量的成分。“截断 SVD”估计使用所有数据，即使存在缺失值。该估计方法使用基于部分奇异值分解的算法，它只计算第一个指定数量的奇异值和奇异值向量。该算法避免计算协方差矩阵以及不必要的主成分，因此计算效率较高，当数据稀疏（即包含很多零时）或当数据中具有大量列时，该算法非常有用。有关统计详细信息，请参见截断 SVD。

注意：这在 JMP 17 之前被称为“稀疏”估计方法。

全部

使用“完全 SVD”估计方法估计所有成分。“完全 SVD”估计不使用含缺失值的观测，因此会排除包含缺失单元格的行。该估计方法使用基于完整奇异值分解的算法。该算法避免计算协方差矩阵，因此计算效率较高，适用于数据中列非常多的情况。有关统计详细信息，请参见完全 SVD。

注意：这在 JMP 17 之前被称为“宽”估计方法。

缺失值插补

（仅当将“宽数据”指定为“方法系列”时才可用。）通过矩阵完成来插补缺失值。

特殊方法

（仅当将“宽数据”指定为“方法系列”并且有指定数量的成分需要估计时才可用。）提供用于计算指定数量的成分的其他方法。

快速近似

使用“随机化奇异值分解”估计指定数量的成分。请参见随机化 SVD。

稳健 PCA

使用一系列奇异值分解和阈值步骤来分解数据矩阵，从而估计指定数量的成分。该方法也用在“探索离群值”平台中。有关“稳健 PCA”方法的详细信息，请参见《预测和专业建模》中的“稳健 PCA 离群值”。

缺失数据

在“主成分”平台中，处理缺失数据的方式取决于方差估计方法。您还可以采用以下方式在平台之外估计缺失值：

• 使用多元方法 > 多元下面的“补缺缺失数据”选项。请参见“补缺缺失数据”。

• 使用分析 > 筛选 > 探索缺失值下面的“多元正态补缺”或“多元 SVD 补缺”实用工具。请参见《预测和专业建模》中的“探索缺失值”。