非参数检验报表
在“单因子”平台中，提供用于比较均值的非参数选项。本节涵盖这些方法的报表。
这些方法包括检验各组间的均值或中位数相等的假设。非参数检验使用响应秩（称为秩得分）函数。请参见 Hajek (1969) 和 SAS Institute Inc. (2020a)。非参数多重比较过程也可用于控制配对比较的总误差率。请参见“非参数多重比较”报表。
Wilcoxon Kruskal - Wallis、中位数、Friedman 秩和 Van der Waerden 检验报表
对于“单因子”平台中的 Wilcoxon Kruskal - Wallis、中位数、Friedman 秩或 Van der Waerden 检验，有两三个表提供汇总统计量和检验结果。汇总统计量表包含以下列：
水平
X 的水平。
计数
每个水平的频数。
得分和
每个水平的秩得分和。
期望得分
在分类水平无差别的原假设下的期望得分。
得分均值
每个水平的均值秩得分。
(Mean-Mean0)/Std0
标准化得分。Mean0 是原假设下期望的均值得分。Std0 是原假设下期望的得分和的标准差。原假设是组均值或中位数在各组之间相等。
Wilcoxon 双样本检验，正态近似表
当 X 变量恰好有两个水平时，“双样本检验，近似正态分布”表包含以下列：
S
观测数较少的水平的秩得分和。
Z
使用 0.5 连续性校正的正态近似检验的检验统计量。请参见双样本正态近似。
概率>|Z|
使用 0.5 连续性校正的正态近似检验的 p 值。该 p 值基于标准正态分布。
Kruskal-Wallis 检验，卡方近似
Kruskal-Wallis 检验表包含位置卡方检验的结果。请参见 Conover (1999)。若组数为 2，则 Kruskal-Wallis 检验等价于 Wilcoxon 检验。
卡方
卡方检验统计量的值。请参见单因子卡方近似。
自由度
检验的自由度。
概率>卡方
检验的 p 值。p 值基于自由度等于 X 水平数减 1 的卡方分布。若组数为 2，该 p 值等于不使用 0.5 连续性校正的正态近似检验的 p 值。
“Kolmogorov-Smirnov 双样本检验”报表
在“单因子”平台中，Kolmogorov-Smirnov 检验报表包含两个表：一个汇总表和一个渐近检验表。汇总表包含以下列：
水平
X 变量的两个水平。
计数
每个水平的频数。
经验分布函数最大值
两个经验累积分布函数 (EDF) 之间差值最大时该 X 变量水平处的 EDF 的值。对于“合计”，该值为两个经验累积分布函数 (EDF) 之间差值最大时该 X 变量值处的合并 EDF（整个数据集的 EDF）的值。
均值偏差最大值
对于每个水平，通过以下步骤获得的值：
‒ 计算给定水平最大值处的 EDF 与合并数据集（合计）最大值处的 EDF 之间的差值。
‒ 用该水平的观测数的平方根乘以该差值。
渐近检验表包含以下列：
KS
Kolmogorov-Smirnov 统计量计算如下：
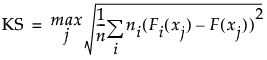
该公式使用以下符号：
‒ xj, j = 1,..., n 为观测
‒ ni 是 X 的第 i 个水平的观测数
‒ F 是合并累积经验分布函数
‒ Fi 是 X 的第 i 个水平的累积经验分布函数
注意：尽管该版本的 Kolmogorov-Smirnov 统计量甚至在 X 变量有两个以上水平时也适用，但在 JMP 中，仅当 X 变量恰好有两个水平时，Kolmogov-Smirnov 选项才可用。
KSa
计算为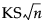 
的渐近 Kolmogorov-Smirnov 统计量，其中，n 是观测总数。
D=max|F1-F2|
两个水平的 EDF 之间的最大绝对偏差。这是通常用于比较两个样本的 Kolmogorov-Smirnov 统计量版本。
概率 > D
检验的 p 值。这是在水平之间没有差异的原假设下 D 超过计算值的概率。
D+ = max(F1-F2)
关于第一组的水平超过第二组的水平的备择假设的单侧检验统计量。
概率 > D+
D+ 检验的 p 值。
D-=max(F2-F1)
关于第二组的水平超过第一组的水平的备择假设的单侧检验统计量。
概率 > D-
D- 检验的 p 值。
“精确检验”报表
当 X 变量恰好有两个水平时，“单因子”平台可为每个非参数检验类型执行精确检验。对于 Wilcoxon Kruskal -Wallis、中位数和 Van der Waerden 精确检验，“双样本：精确检验”表包含以下列：
S
较小组中观测的秩得分和。若 X 的两个水平有相同的观测数，则 S 值对应于值排序中 X 的最后一个水平。
概率 £ S
检验的单侧 p 值。
概率 ≥ |S-Mean|
检验的双侧 p 值。
注意：对于 Kolmogorov-Smirnov 精确检验，该表提供与渐近检验相同的统计量。不过，计算的 p 值为精确值。请参见“Kolmogorov-Smirnov 双样本检验”报表。