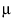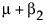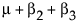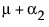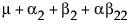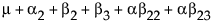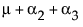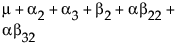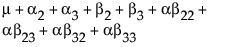有序型因子

在“拟合模型”平台中，使用有序型建模类型标记的因子的编码方式不同于名义型因子的编码方式。这些参数估计值的解释不一样，检验不同并且最小二乘均值不同。

对于有序型因子，因子的第一个水平是控制或基线水平，参数测量将有序型因子设置为每个后续水平时对响应的影响。有序型因子编码适用于包含表示各种剂量水平的因子，其中第一个剂量为零。下表显示了一个三水平有序型因子的示例：

设计的模式为：下三角处是 1，在别处为 0。

对于简单的主效应模型，这可以指定如下：

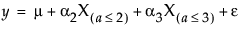
请注意，m 是 A = 1 处的期望响应，m + a2 是 A = 2 处的期望响应，m + a2 + a3 是 A = 3 处的期望响应。因此，a2 估计从 A = 1 移到 A = 2 的效应，a3 估计从 A = 2 移到 A = 3 的效应。

若有序型主效应的所有参数具有相同符号，则响应效应在有序型水平上是单调的。

有序型交互作用

有序型交互作用与名义型效应一样，从因子各列的水平方向的直积得来。考虑一个示例，它有两个有序型因子 A 和 B，每个因子具有三个水平。JMP 的有序型编码生成下面所示的设计矩阵。交互作用的模式是下三角矩阵为 1 的分块下三角矩阵。

注意：当您检验是否没有效应时，对于简单模型的名义型和有序型因子没有太大的差异。但是，指定交互作用时，就有很大差异了。对于大多数模型，我们建议您使用名义型因子而非有序型因子。

有序型交叉模型的假设检验

要了解参数的含义，请查看这个使用参数的期望单元格均值的表，其中 m 是截距，a2 是水平 A2 的参数等等。

请注意，A 的主效应检验实际上检验 B 固定在第一个水平时的 A 水平。类似地，B 的主效应检验将 A 固定在第一个水平下在 B 的各个水平的顶部行之间检验。该检验适用于两个因子是不同治疗的剂量的实验。主要问题是每个治疗本身的效力，当采用两种药物的剂量时，很少有人关注药物交互作用。在某些情况下，每种药物采用大剂量还可能是危险的。

请注意，可以通过添加与自身左上方的每个单元格（包括当前行和列）关联的所有参数，得到每个单元格的期望值。最后一个单元格的期望值是所有参数之和。

尽管包含在其他效应中的效应的假设检验在有序型和名义型编码方面不同，但是不包含在其他效应中的效应的检验是相同的。在上述交叉设计中，无论 A 和 B 是名义拟合还是有序拟合，交互作用的检验都是相同的。

有序型最小二乘均值

如前文所述，在将所有其他因子设置为某个中性值后，最小二乘均值是对应于某个水平组合的预测值。JMP 将具有未涉及的有序型因子的效应的中性值定义为在第一个水平（即“控制”或基线水平）下的效应。

这个有序型因子的最小二乘均值定义主张该观点：被包含效应的假设检验等价于检验最小二乘均值是相等的。

有序型效应中的奇异性和缺失单元格

使用有序型编码，您将指定有序型效应的第一个水平是基线。因此可以获得对主效应的良好检验，即使当交互作用中有缺失单元格时（即使您没有交互作用的数据时）也是如此。

具有缺失单元格的示例

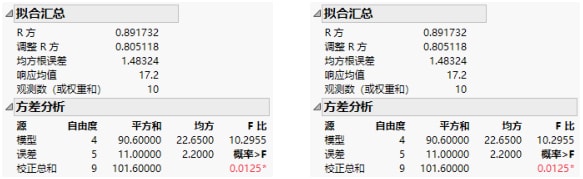
该示例与上例相同，每个单元格有两个观测值，但是 A3B2 单元格没有数据。您现在可以比较以名义方式对因子编码时的结果和以有序方式对因子编码时的结果。模型拟合是相同的，如图 A.2 中所示。

图 A.2 名义型因子（左侧）和有序型因子（右侧）的汇总信息 

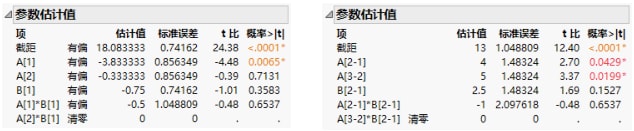
因为编码方式不同，参数估计值相差很大。请注意，缺失单元格影响名义型参数的可估性但不影响有序型参数的可估性。

图 A.3 名义型因子（左侧）和有序型因子（右侧）的参数估计值 

奇异性详细信息显示线性相依性（也通过检查这些值来标识缺失单元格）。

图 A.4 名义型因子（左侧）和有序型因子（右侧）的奇异性详细信息 

名义型的效应检验损失自由度。在 B 中，没有检验。对于有序型，没有损失，因为对于基本的第一个水平没有缺失单元格。

图 A.5 名义型因子（左侧）和有序型因子（右侧）的效应检验 

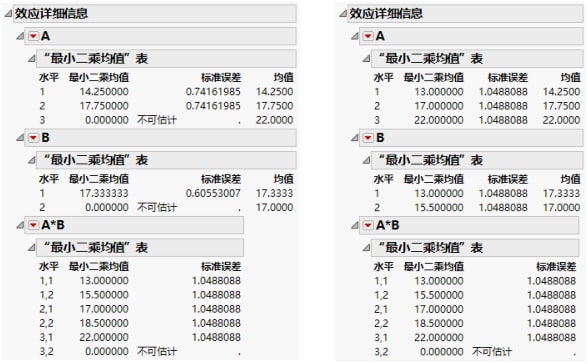
最小二乘均值也不同。有些名义型 LSM 不可估计，但是有序型 LSM 都可以估计。您可以通过查看单元格均值来验证这些值。请注意 A*B LSM 对于名义型和有序型是相同的。图 A.6 显示名义型和有序型因子的最小二乘均值。

图 A.6 名义型因子（左侧）和有序型因子（右侧）的最小二乘均值 

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).