功效报表
在“单因子”平台中,“功效”选项计算统计功效以及有关给定假设检验的其他细节。请参见“功效”选项的示例。有关统计详细信息,请参见功效的统计详细信息。
• LSV(最小显著性值)是一些参数或参数函数的值,其产生某一 p 值 alpha。即您要了解在某个 p 值 alpha 下多小的效应可被称为显著。LSV 提供了以参数尺度而非概率尺度测量显著性的方法。它显示设计和数据的敏感程度。
• LSN(最小显著性数)是在数据采用相同形式的情况下将生成指定 p 值 alpha 的总观测数。LSN 定义为在给定的 alpha、sigma 和 delta 值的情况下(即显著性水平、误差的标准差和效应大小)减少估计值方差以实现显著性结果所需的观测数。若您需要更多数据来实现显著性,LSN 可帮助告知还需要多少数据。LSN 是生成约 50% 功效的总观测数。
• 功效是当两个组存在真正差异时获得显著性(p 值 < alpha)的概率。它是样本大小、效应大小、误差的标准差和显著性水平的函数。功效告知您的实验在给定的 alpha 水平下有多大可能检测到差异(效应大小)。
注意:单因子布局中仅有两个组时,功效工具所计算的 LSV 与多重比较表中所示的最小显著性差异 (LSD) 相同。
功效详细信息
“单因子”平台中的“功效详细信息”窗口和表与“拟合模型”平台中的窗口和表是相同的。有关功效计算的详细信息,请参见《拟合线性模型》中的“功效计算”。
对于四个列 Alpha、Sigma、Delta 和个数,请分别填写一个值、两个值或一系列值的初值、终值和增量(图 6.29)。对您指定值的所有可能组合执行功效计算。
Alpha (a)
显著性水平,介于 0 到 1 之间(通常为 0.05、0.01 或 0.10)。最初显示值 0.05。
Sigma (s)
模型中剩余误差的标准误差。最初在此处提供 RMSE,即误差的均方平方根的估计值。
Delta (d)
原始效应大小。有关效应大小计算的详细信息,请参见《拟合线性模型》中的“效应大小”。第一个位置最初设置为假设的平方和除以 n 所得值的平方根(即 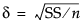 )。
)。
个数 (n)
所有组的总样本大小。最初在第一个位置存放实际样本大小。
功效求解
将功效(显著性结果的概率)作为以下四个值的函数求解:a、s、d 和 n。
最小显著数求解
在给定 a、s 和 d 的情况下求解实现约 50% 的功效所需的观测数。
最小显著值求解
求解生成 a 的 p 值的参数或线性检验的值。它是 a、s、n 和估计值的标准误差的函数。仅当 X 变量恰好有两个水平且通常用于单个参数时,才可使用该功能。
调整功效和置信区间
要追溯了解功效时,可以使用标准误差和检验参数的估计值。
‒ 调整功效是从非中心参数的更加无偏估计值计算的功效。
‒ 调整功效的置信区间基于非中心估计值的置信区间。
仅对原始 Delta 计算调整功效和置信限,因为其中存在随机变异。