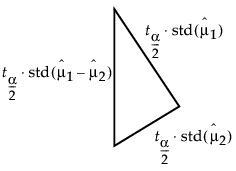比较环的统计详细信息

在“单因子”平台中，比较环是多重比较检验中最小显著性差异 (LSD) 的图形化表示。该最小显著性差异是概率分位数与两个均值差值的标准误差的乘积。对于“每对”选项，将使用 Fisher LSD 并且概率分位数是 Student t 统计量。针对该情况演示了比较环计算。LSD 定义如下：

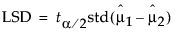
根据以下关系计算两个独立均值的差值的标准误差：

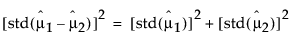
均值不相关时，这些量之间具有以下关系：

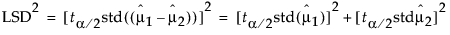
这些平方值构成了勾股定理关系，图 6.41 中所示的直角三角形对此进行了说明。

图 6.41 两个均值之间的差值的关系 

该直角三角形的斜边是比较均值的量尺。仅当实际差值大于直角三角形的斜边 (LSD) 时，均值存在显著差异。

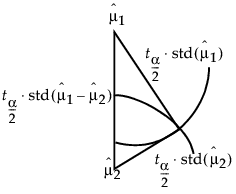
假定您在边界线上正好有两个均值，其中实际差值与最小显著性差异相同。使用在垂直尺度上测量的均值为顶点绘制三角形。此外，在每个均值周围绘制圆，使每个圆的直径等于该均值的置信区间。

图 6.42 t 检验统计量的几何关系 

每个圆的半径是三角形相应直角边的长度，即 。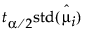

两个直角边相交成一直角，这些圆也在同一点相交成同一直角，给出以下关系：

• 若均值差值刚好等于最小显著性差异，则每个均值周围的置信区间圆相交为直角。即切线的角为直角。

现在，考虑均值差值大于或小于最小显著性差异时这些圆应如何相交：

• 若圆相交导致外角大于直角，则均值不存在显著差异。若圆相交导致外角小于直角，则均值存在显著差异。外角小于 90 度表示均值分开的距离超过最小显著性差异。

• 若圆不相交，则均值存在显著差异。若圆嵌套，则均值没有显著差异（图 6.9）。

同样的图形方法适用于很多多重比较检验，用 Student t 的不同概率分位数值替代即可。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).