限值的统计详细信息
在“模型驱动的多元控制图”平台中，当启动窗口中未指定历史行数时，所有数据都被视为历史数据。请参见启动“模型驱动的多元控制图”平台。
T2
历史数据的上控制限 (UCL) 基于 Beta 分布并定义如下：
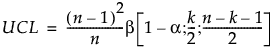
其中：
n = 历史数据观测数
k = PCA 或 PLS 成分数
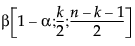= Beta
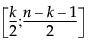分布的第 (1−a) 分位数。
当前数据的上控制限基于 F 分布并定义如下：
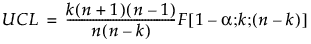
其中：
n = 历史数据观测数
k = PCA 或 PLS 成分数
F(1−a; k; n−k) = F(k; n−k) 分布的第 (1−a) 分位数。
DModX
对于 PCA 和 PLS 模型，上控制限基于 F 分布。PCA 模型的 DModX 上控制限定义为：
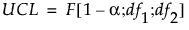
其中：
df1 = p−k
df2 = (n−k−1)(p−k)（若数据已中心化）；或为 (n−k)(p−k)（若数据未中心化）
n = 历史数据观测数
k = PCA 成分数
p = 变量数
F(1−a; n−p−1; p−k) = F(n−p−1; p−k) 分布的第 (1−a) 分位数
PLS 模型的 DModX 上控制限定义为：
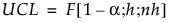
其中：
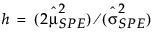
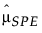= SPE 的历史样本均值
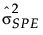= SPE 的历史样本方差
n = 历史数据观测数
F(1−a; h; nh) = F(h; nh) 分布的第 (1−a) 分位数。
SPE
PCA 模型的 SPE 上控制限定义为：
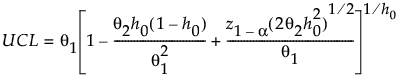
其中：
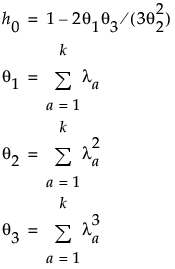
la = 第 a 个特征值
k = PCA 成分数
z1−α = 标准正态分布的第 (1−a) 分位数
有关用于 PCA 模型的 SPE 控制限的详细信息，请参见 Jackson and Mudholkar (1979)。
对于 PLS 模型，上控制限基于卡方分布并定义如下：
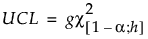
其中
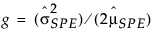
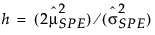
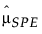= SPE 的历史样本均值
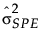= SPE 的历史样本方差
c2(1−a; h) = c2(h) 分布的第 (1−a) 分位数
g 和 h 参数通过矩量法估计。有关用于 PCA 模型的 SPE 控制限的详细信息，请参见 Nomikos (1995)。