不等方差报表
“单因子”平台提供检验组方差是否相等的四个检验。不相等方差的前三个检验的概念是对构造用于测量每个组的离散程度的新响应变量执行方差分析。第四个检验为 Bartlett 检验,它类似于正态分布下的似然比检验。在启动窗口中指定“区组”变量时,“不等方差”选项不可用。
注意:用于不等方差的另一检验方法为 ANOMV。请参见“均值分析”报表。
以下相等方差检验可用:
O’Brien
构造因变量,使新变量的组均值等于原始响应的组样本方差。对 O’Brien 变量的方差分析实际是对组样本方差的方差分析(O’Brien 1979;Olejnik and Algina 1987)。
Brown-Forsythe
显示方差分析的 F 检验,其中响应是每个观测与组中位数差值的绝对值 (Brown and Forsythe 1974)。
Levene
显示方差分析的 F 检验,其中响应是每个观测与组均值差值的绝对值 (Levene 1960)。离散程度的计算公式为 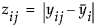 。
。
Bartlett
比较样本方差的加权算术平均值与样本方差的加权几何平均值。几何平均值始终小于或等于算术平均值,仅在所有样本方差相等时才保持相等性。组方差之间的变异越大,这两个平均值的差异越大。创建这两个平均值的函数,它近似服从 c2 分布(或实际为某个公式下的 F 分布)。大值对应于算术或几何比的大值,因此对应于变异范围很宽的组方差。Bartlett 卡方检验统计量除以自由度得到表中所示的 F 值。Bartlett 检验对于违反正态分布假定的情况不是很稳健 (Bartlett and Kendall 1946)。
F 检验双侧
(仅当 X 变量具有两个水平时才可用。)若仅检验两个组,则还执行针对不等方差的标准 F 检验。F 检验是较大方差与较小方差估计值之比。将 F 分布的 p 值加倍可以使它成为双侧检验。
注意:若指定了区组列,则对进行了区组均值调整的数据执行方差检验。
请参见“不等方差”选项的示例。
提示:若不等方差检验指示组方差有显著差异,请考虑 Welch 检验替代标准的方差分析检验。Welch 统计量基于通常的方差分析 F 检验。但是,均值使用组均值方差的倒数进行加权(Welch 1951;Brown and Forsythe 1974;Asiribo and Gurland 1990)。若只有两个水平,则 Welch 方差分析等价于不等方差 t 检验。
“等方差检验”报表
在“单因子”平台中,“等方差检验”报表显示一个标准差图并提供汇总表。第一个表包含以下列:
水平
数据中出现的因子水平。
计数
每个水平的频数。
标准差
每个因子水平对应响应的标准差。标准差等于 O’Brien 变量的均值。若水平仅在数据中出现一次,则不计算标准差。
相对均值的绝对差值平均值
响应和组均值的绝对差值平均值。绝对差值平均值等于 Levene 变量的组均值。
相对中位数的绝对差值平均值
响应和组中位数的绝对差值平均值。绝对差值平均值等于 Brown-Forsythe 变量的组均值。
第二个表汇总等方差检验并包含以下列:
检验
每个检验的名称。
F 比
计算得出的 F 统计量。请参见等方差检验的统计详细信息。
分子自由度
分子的自由度。若因子具有 k 个水平,则分子具有 k - 1 个自由度。在计算 O’Brien、Brown-Forsythe 或 Levene 的检验统计量时,不使用在数据中只出现一次的水平。此情况下的分子自由度是计算中使用的水平数减 1。
分母自由度
分母中使用的自由度。对于 O’Brien、Brown-Forsythe 和 Levene,用于计算检验统计量的每个因子水平都要扣除一个自由度。若因子具有 k 个水平,则分母自由度为 n - k。
p 值
得到 F 比值大于计算出的 F 比值(当方差在所有水平上都相等时计算出的)的概率。
注意:若 X 变量的任何水平包含的观测不足 5 个,则会显示一条警告。有关以上样本较小的检验的性能的详细信息,请参见 Brown and Forsythe (1974) 和 Miller (1972)。
“Welch 检验”报表
F 比
等均值检验的 F 检验统计量。
分子自由度
检验的分子的自由度。若因子具有 k 个水平,则分子具有 k - 1 个自由度。在计算 Welch 方差分析时,不使用在数据中只出现一次的水平。此情况下的分子自由度是计算中使用的水平数减 1。
分母自由度
检验的分母的自由度。请参见等方差检验的统计详细信息。
概率>F
得到 F 比值大于计算出的 F 比值(当均值在所有水平上都相等时计算出的)的概率。
t 检验
(仅当 X 变量恰好有两个水平时才可用。)显示 F 比和 t 检验之间的关系。计算为 F 比的平方根。