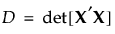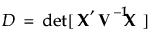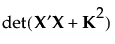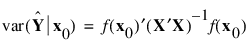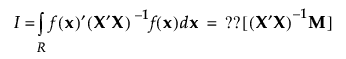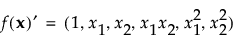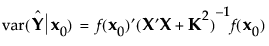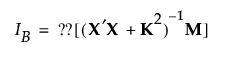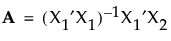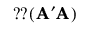最优性准则

本节提供有关以下设计的信息：

•

D 最优性

•

•

•

•

•

默认情况下，“定制设计”平台优化 D 最优性准则，除非使用“RSM”按钮创建了完全二次模型。这种情况下会构造 I 最优设计。

D 最优性准则将模型系数估计值的协方差矩阵的行列式最小化。由此断定 D 最优性着重于对效应的精确估计。该准则在以下情况下较为理想：

•

筛选设计

•

侧重于估计效应或检验显著性的实验

•

标识活跃因子是实验目标的设计

D 最优性准则依赖于假设模型。这造成了一定的局限性，因为真正模型的形式往往事先不可知。D 最优设计的试验优化假设模型的系数精度。在极端情况下，D 最优设计可能饱和，试验次数即参数个数，没有失拟自由度。

具体而言，D 最优设计最大化 D，其中，D 定义如下：

其中，X 是在模拟响应中定义的模型矩阵。

D 最优裂区设计最大化 D，其中，D 定义如下：

V -1 是响应的区组对角协方差矩阵 (Goos 2002)。

由于 D 最优设计侧重于最小化系数的标准误差，所以可能不允许检查模型是否正确。例如，D 最优设计在一阶模型中不包含中心点。若存在可能活跃的项未包含在假设模型中，更好的方法是指定“若可能”项并使用 Bayesian D 最优设计。

Bayesian D 最优性

Bayesian D 最优性是经过修改的 D 最优性准则。Bayesian D 最优性准则在存在可能活跃的交互作用或非线性效应的情况下很有用。请参见 DuMouchel and Jones (1994) 以及 Jones et al (2008)。

Bayesian D 最优性可准确估计指定的一组模型参数。这些是您在“模型”分级显示项中将“可估计性”指定为“必需”的效应。但同时，Bayesian D 最优性有能力估计其他效应，通常为高阶效应（在试验规模允许的情况下）。这些是您在“模型”分级显示项中将“可估计性”指定为“若可能”的效应。Bayesian D 最优设计会在试验规模限制所允许的最大范围内，允许检测仅包含“必需”效应的模型中的不充分性。

在试验次数大于“必需”项个数但小于“必需”项与“若可能”项个数之和的情况下，Bayesian D 最优性准则最为有效。若出现这种情况，试验次数小于您要估计的参数个数。使用 Bayesian 设置中的先验信息允许精确估计所有“必需”项，同时提供检测和估计某些“若可能”项的能力。

要允许将有意义的先验分布应用到模型参数，需要对响应和因子的尺度进行统一以具备特定属性 (DuMouchel and Jones 1994, Section 2.2)。

使用以下符号：

•

X 是在模拟响应中定义的模型矩阵

•

K 是具有以下值的对角矩阵：

‒

k = 0 代表“必需”项

‒

k = 1 代表涉及含有两个以上水平的分类因子的“若可能”主效应、幂和交互作用

‒

k = 4 代表其他所有“若可能”项

对“若可能”参数的向量施加的先验分布属于多元正态分布，均值向量为 0 并且对角协方差矩阵包含 1/k2 个对角线元素。因此，值 k2 是相应参数先验方差的倒数。

k 的值凭经验决定。对于“若可能”主效应、幂和具有多个自由度的交互作用，其先验方差为 1。其他“若可能”项的先验方差为 1/16。在 DuMouchel and Jones (1994) 采用的符号表示法中，k = 1/τ。

要控制“若可能”项的权重，请从红色小三角菜单中选择高级选项 > 先验参数方差。请参见高级选项 > 先验参数方差。

参数的后验分布具有协方差矩阵 (X’X + K2)-1。通过将后验协方差矩阵的逆矩阵的行列式最大化，可获得 Bayesian D 最优设计：

I 最优性

I 最优设计可最小化设计空间上的预测平均方差。若您的主要实验目标不是估计系数，而是执行以下操作，则 I 最优性准则比 D 最优性更合适：

•

预测响应

•

确定最佳操作条件

•

确定设计空间中响应落在可接受范围内的区域

在以上情况下，响应的精确预测优先于参数的精确估计。

在设计空间中的 x0 点处，相对于未知误差方差的预测方差可计算如下：

其中，X 是在模拟响应中定义的模型矩阵。

I 最优设计在整个设计空间上将预测方差的积分 I 最小化，其中，I 计算如下：

此处 M 是矩量矩阵：

请参见模拟响应。有关进一步的详细信息，请参见 Goos and Jones (2011b)。

矩量矩阵不依赖设计，可提前计算。行向量 f (x)’ 包含 1，后跟与假设模型对应的效应。例如，对于含有两个连续因子的完全二次模型，f (x)’ 定义如下：

A 最优性

A 最优性准则将模型系数估计值的协方差矩阵的迹最小化。迹就是矩阵的主对角线元素的总和。A 最优设计可使回归系数的方差之和最小。

Bayesian I 最优性

Bayesian I 最优设计可将设计区域中“必需”和“若可能”项的平均预测方差最小化。

使用以下符号：

•

X 是在模拟响应中定义的模型矩阵

•

K 是具有以下值的对角矩阵：

‒

k = 0 代表“必需”项

‒

k = 1 代表涉及含有两个以上水平的分类因子的“若可能”主效应、幂和交互作用

‒

k = 4 代表其他所有“若可能”项

对“若可能”参数的向量施加的先验分布属于多元正态分布，均值向量为 0 并且对角协方差矩阵包含 1/k2 个对角线元素。（请参见Bayesian D 最优性，了解有关值 k 的更多详细信息。）

x0 点处的预测值后验方差如下所示：

Bayesian I 最优设计可将设计区域中的平均预测方差最小化，如下所示：

其中，M 是矩量矩阵。请参见模拟响应。

别名最优性

别名最优性的目的在于：将假设模型中的效应与该模型中不存在但可能活跃的效应之间的别名关系最小化。模型中不存在但可能需要关注的效应称为别名效应。有关别名最优设计的详细信息，请参见 Jones and Nachtsheim (2011b)。

具体而言，令 X1 成为与假设模型中的项对应的模型矩阵，如模拟响应中定义。该设计定义与别名效应对应的模型。将别名效应的模型项矩阵表示为 X2。

别名矩阵是矩阵 A，定义如下：

别名矩阵中的条目代表与模型项估计值关联的偏倚度。请参见别名矩阵，了解别名矩阵的由来。

A 中条目的平方和提供了偏倚的汇总测度。该平方和可以使用迹形式表示，如下所示：

通常，减小迹准则的设计的 D 效率比 D 最优设计要低。因此，别名最优性寻求在受制于 D 效率下限的前提下将 A’A 的迹最小化。有关 D 效率的定义，请参见最优性准则。D 效率的下限通过 D 效率权重给出，可在“高级选项”下指定该权重。请参见高级选项 > D 效率权重。