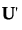 表示矩阵 U 的转置矩阵。
表示矩阵 U 的转置矩阵。用 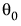 表示算法终止时的
表示算法终止时的 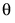 值。请注意在
值。请注意在 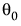 处计算出的相对梯度为得分检验统计量。使用具有 k 个自由度的卡方分布计算 p 值。该 p 值指示未知的 MLE 值是否与
处计算出的相对梯度为得分检验统计量。使用具有 k 个自由度的卡方分布计算 p 值。该 p 值指示未知的 MLE 值是否与 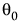 一致。“随机效应协方差参数估计值”报表中列出的无界参数数目等于 k。
一致。“随机效应协方差参数估计值”报表中列出的无界参数数目等于 k。
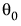 表示算法终止时的
表示算法终止时的 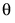 值。请注意在
值。请注意在 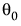 处计算出的相对梯度为得分检验统计量。使用具有 k 个自由度的卡方分布计算 p 值。该 p 值指示未知的 MLE 值是否与
处计算出的相对梯度为得分检验统计量。使用具有 k 个自由度的卡方分布计算 p 值。该 p 值指示未知的 MLE 值是否与 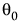 一致。“随机效应协方差参数估计值”报表中列出的无界参数数目等于 k。
一致。“随机效应协方差参数估计值”报表中列出的无界参数数目等于 k。 收敛得分检验
收敛得分检验 得分检验
得分检验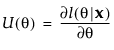
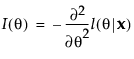
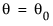 的得分检验的统计量为:
的得分检验的统计量为: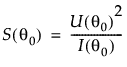
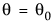 的得分检验的检验统计量为:
的得分检验的检验统计量为: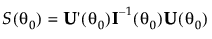
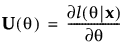
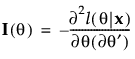
 相对梯度
相对梯度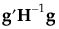 。此处
。此处 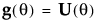 是对数似然函数的梯度,
是对数似然函数的梯度,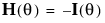 是它的 Hessian。
是它的 Hessian。