为使用 Tukey-Kramer HSD(真实显著性差异)检验 (Tukey 1953; Kramer 1956) 执行的最小二乘均值配对比较显示检验和置信区间。请参见最小二乘均值 Student t 和最小二乘均值 Tukey HSD。
最小二乘均值是在其他模型因子均设置为中性值的情况下,模型针对某个分类效应的水平预测的值。连续效应的中性值定义为其样本均值。关注的效应中未涉及的名义型效应的中性值是该效应的系数平均值。未涉及的有序型效应的中性值定义为值排序中的第一个效应水平。
最小二乘均值亦称调整均值或总体边缘均值。若模型中还有其他效应,最小二乘均值可能与简单均值不同。事实上,常常可以看到各最小二乘均值比起各样本均值来说,靠得更近。这种情形是由于做出预测处的中性值的性质导致的。
由于最小二乘均值是其他模型因子的特定值处的预测,所以您可以比较它们。检验效应时,将使用最小二乘均值进行比较。有关最小二乘均值的更多详细信息,请参见名义型因子的最小二乘均值和第 449 页的“有序型最小二乘均值”。
|
1.
|
|
2.
|
选择分析 > 拟合模型。
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
点击运行。
|
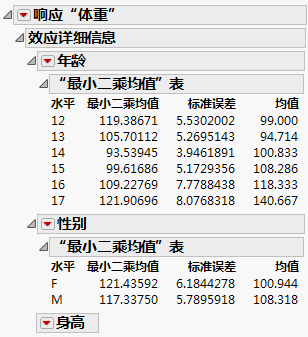
图 3.10 最小二乘均值表
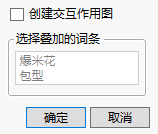
图 3.11 “最小二乘均值图选项”窗口
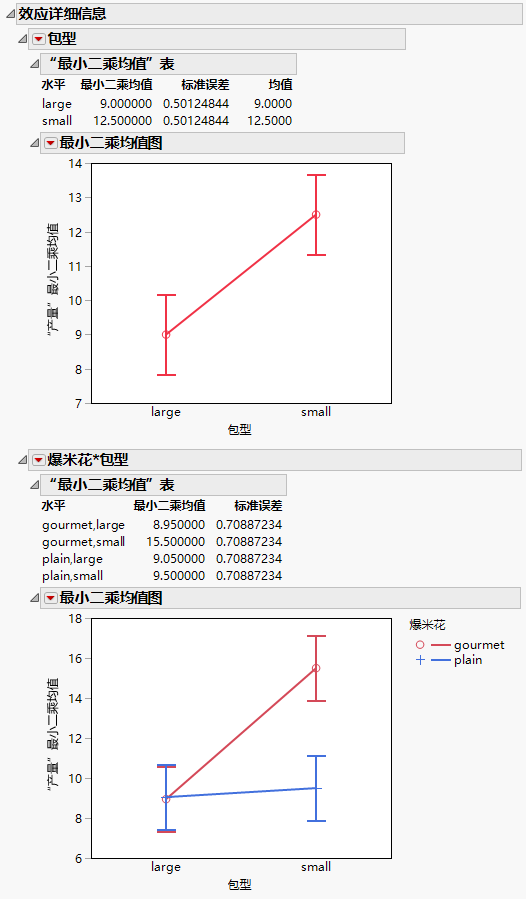
图 3.12 两个效应的最小二乘均值表和图
|
1.
|
|
2.
|
选择分析 > 拟合模型。
|
|
3.
|
|
4.
|
|
5.
|
点击运行。
|
|
7.
|
|
8.
|
|
10.
|
在“选择叠加的词条”下,选择爆米花。
|
|
11.
|
点击确定。
|
|
13.
|
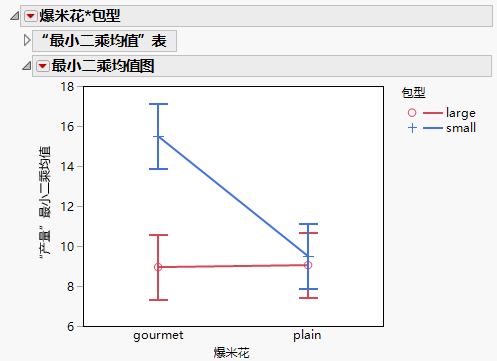
图 3.13 转置了因子的交互作用的最小二乘均值图
每次您点击 + 或 - 按钮时,对比系数都进行标准化,尽可能使其总和为 0 且其绝对值总和等于 2。要比较其他水平,请点击新建列按钮。随即显示一个新列,您可以在其中定义新对比。完成操作后,点击完成。“对比”报表随即显示(图 3.15)。总体检验是一个针对所有对比的联合 F 检验。
“对比”报表提供以下关于联合 F 检验的详细信息:
显著性检验的 p 值
|
1.
|
|
2.
|
选择分析 > 拟合模型。
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
点击运行。
|
|
7.
|
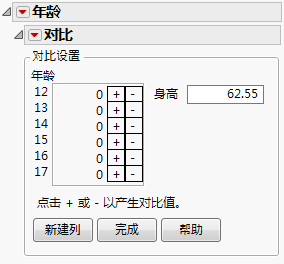
图 3.14所示的“对比设置”报表随即显示。
图 3.14 “年龄”的最小二乘均值对比设置
|
10.
|
请注意,连续效应身高旁边有一个文本框。默认值是连续效应的均值。
|
|
11.
|
点击完成。
|
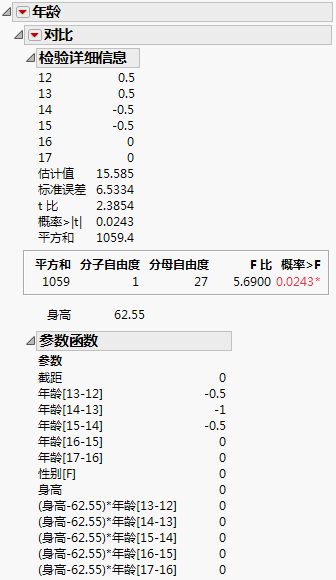
“对比”报表显示在图 3.15中。对比检验在 0.05 水平下显著。您可以得出结论:身高均值为 62.55 时,年龄为 12 岁和 13 岁的少年的体重预测值在统计上与年龄为 14 岁和 15 岁的少年的体重预测值存在差异。
图 3.15 最小二乘均值“对比”报表
最小二乘均值 Student t 和最小二乘均值 Tukey HSD(真实显著性差异)选项检验模型效应的配对比较。
|
•
|
“最小二乘均值 Student t”选项是基于通常的独立样本的等方差 t 检验。每个比较基于指定的显著性水平。执行多重比较得到的总误差率超过这个指定的显著性水平。
|
|
•
|
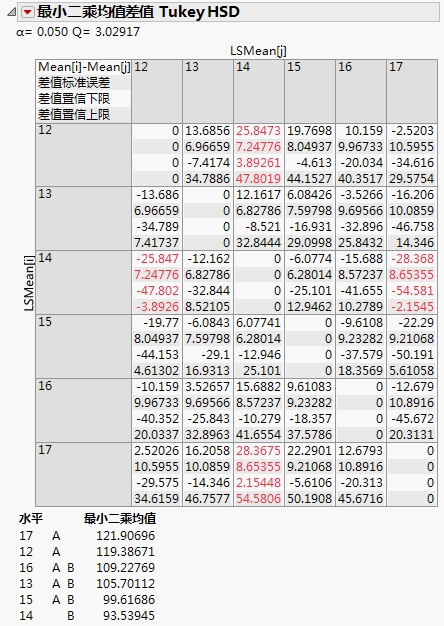
图 3.16显示了 Big Class.jmp 样本数据表中年龄效应的“最小二乘均值 Tukey”报表。(通过运行拟合模型数据表脚本并从年龄的红色小三角菜单中选择最小二乘均值 Tukey HSD,您可以获取该报表。)默认情况下,该报表显示“交叉表报表”和“连接字母报表”。
图 3.16 “最小二乘均值 Tukey HSD”报表
在图 3.16中,水平 17、12、16、13 和 15 由字母 A 连接。该连接指示这些水平在 0.05 显著性水平下无差异。同样,水平 16、13、15 和 14 由字母 B 连接,指示它们在统计上无差异。但是,年龄 17 和 14 以及年龄 12 和 14 没有由公共字母连接,这指示这两对水平在统计上有差异。
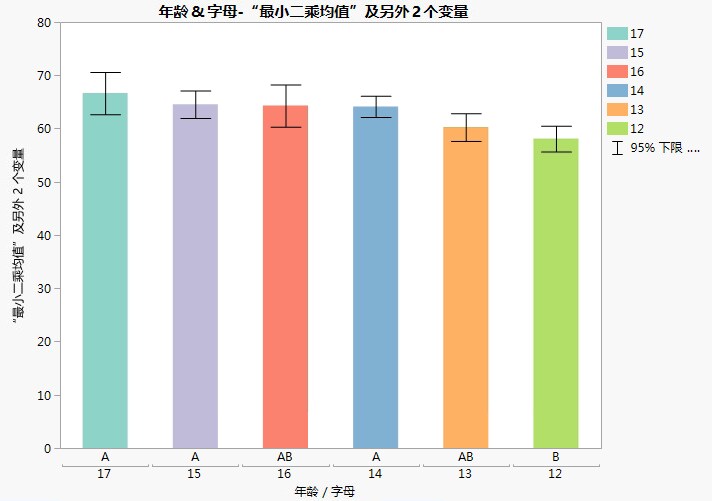
图 3.17显示了基于 Big Class.jmp 的示例的条形图。运行拟合模型数据表脚本,从年龄的红色小三角菜单中选择最小二乘均值 Tukey HSD。从“最小二乘均值差值 Tukey HSD”报表中选择保存连接字母表。在显示的数据表中运行条形图脚本。
按从大到小的顺序对差值排名,提供标准误差、置信限和 p 值。同时在条形图上标绘差值,且置信区间叠加在一起。
为每个比较提供单个详细报表。对于给定比较,该报表显示估计差值、标准误差、置信区间、t 比、自由度以及单侧和双侧检验的 p 值。同时还显示 t 分布图,该图演示比较的显著性检验。着色部分的区域是双侧检验的 p 值。
图 3.17 最小二乘均值差值 HSD 连接字母表中的条形图
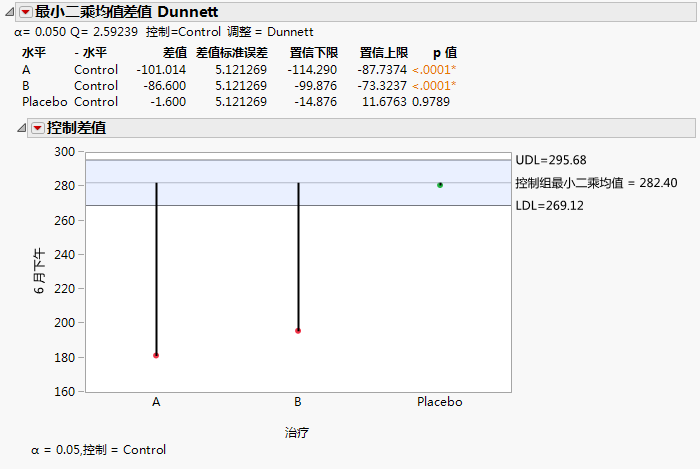
Dunnett 检验 (Dunnett 1955) 将一组均值与控制组的均值进行比较。误差率应用于配对比较集合。“最小二乘均值 Dunnett”选项针对给定效应的水平执行 Dunnett 检验。使用 Hsu 因子分析近似来计算 p 值和置信区间 (Hsu 1992)。
图 3.18 “最小二乘均值 Dunnett”报表
打开“功效详细信息”窗口,您可以在该窗口中输入信息以获取特定效应的 F 检验的回顾或前瞻详细信息。
注意:要确保您的研究所包含的观测数足以检测所需的差值,请在设计实验时使用关于功效的信息。这种分析称为前瞻功效分析。请考虑使用“实验设计”平台来设计您的研究。“实验设计”>“样本大小与功效”和“实验设计”>“评估设计”都有助于前瞻功效分析。有关使用标准最小二乘法的前瞻功效分析的示例,请参见前瞻功效分析。
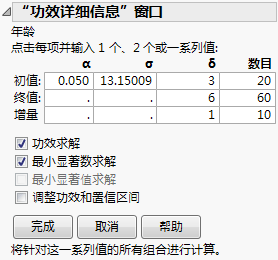
图 3.19显示了 Big Class.jmp 样本数据表的“功效详细信息”窗口的示例。使用“功效详细信息”窗口,您可以探索 alpha (α)、sigma (σ)、delta (δ) 和“数目”(研究规模)值的功效。输入单个值(仅“初值”)、两个值(“初值”和“终值”),或是对一系列值输入起始值(初值)、终止值(终值)以及增加值(增量)。将为您指定的值的所有可能组合报告功效计算。
图 3.19 “功效详细信息”窗口
Alpha (α)
Sigma (σ)
Delta (δ)
数目 (n)
回顾功效计算使用标准误差估计值,以及估计 F 分布的非中心参数时使用的检验参数的估计值。调整功效是基于非中心参数的估计值(已去除正偏倚)的回顾功效计算 (Wright and O’Brien 1988)。
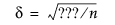 。
。