随机效应模型是所有因子都表示随机效应的模型。(请参见随机效应。)此类模型亦称方差分量模型。随机效应模型往往是分层模型。同时包含固定和随机效应的模型称为混合模型。重复测量和裂区模型是混合模型的特例。通常使用混合模型一词来包含随机效应模型。
要拟合混合模型,您必须在“拟合模型”启动窗口中指定随机效应。不过,若所有模型效应都是随机的,您还可以在“变异性 / 计数量具图”平台中拟合模型。只能在该平台中拟合特定模型。请注意,在“变异性 / 计数量具图”平台中使用的拟合方法不允许方差分量估计值为负。有关“变异性 / 计数量具图”平台如何拟合方差分量模型的详细信息,请参见《质量和过程方法》手册中的“变异性量具图”和“计数量具图”。
随机效应是其水平被视为某个总体中的随机样本的因子。通常,随机效应的精确水平并不受关注,而水平反映出的变异才受关注(方差分量)。不过,也有些时候您想要预测随机效应给定水平的响应。更严格地来讲,随机效应被视为服从均值为零且方差非零的正态分布。
|
•
|
|
•
|
|
•
|
|
•
|
|
•
|
|
•
|
|
•
|
|
•
|
|
•
|
γ 和 ε 不相关
|
|
•
|
REML 表示限制最大似然(始终为推荐方法)
|
|
•
|
EMS 表示期望均方(仅适用于旧版教科书的教学)
|
REML 方法现已取代传统 EMS 方法成为主流的拟合方法。与 EMS 方法相比,REML 在适用性方面要广泛得多。REML 方法最早是由 Patterson and Thompson (1974) 提出的。另见 Wolfinger et al. (1994) 和 Searle et al. (1992)。
EMS 方法,亦称矩量法,是在功能强大的计算机面世之前开发出来的。研究人员将自己限定在平衡环境中,并使用 EMS 方法(提供了计算快捷方式)来计算随机效应的估计值和混合模型。由于当今仍在使用的许多教科书仍使用 EMS 方法来介绍包含随机效应的模型,所以 JMP 提供了 EMS 选项。(请参见,例如 McCulloch et al., 2008; Poduri, 1997; Searle et al., 1992。)
在“拟合模型”启动窗口中指定包含随机效应的模型。要指定随机效应,在“构造模型效应”列表中将其突出显示,然后选择特性 > 随机效应。这将向模型效应列表中的效应名称后附加上“&随机”。(有关随机效应的定义,请参见随机效应。)还可以在单独的效应选项卡中指定随机效应。(请参见“模型规格”一章中第 27 页的““构造模型效应”选项卡”。)
若您关注的是固定效应,则应保持选定“无界限方差分量”选项。将方差估计值限制为非负将导致固定效应检验发生偏倚。
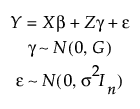
 “混合模型”特质拟合众多协方差结构,包括残差、一阶自回归(或
“混合模型”特质拟合众多协方差结构,包括残差、一阶自回归(或