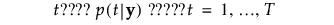本节给出通过得分选项 > 保存公式保存的推导公式。这些公式依赖于判别方法。
|
nt
|
第 t 组中的观测数
|
|
ybar
|
|
|
qt
|
组 t 的成员关系的先验概率
|
|
y 属于组 t 的后验概率
|
|
|
|A|
|
按以下方式计算组 t 的成员关系的后验概率:
观测 y 被分配给具有最大后验概率的组。
|
SqDist[<组 t>]
|
|
|
Prob[<组 t>]
|
|
|
Pred <X>
|
在二次判别分析中,不假定组内协方差矩阵是相等的。组 t 的组内协方差矩阵由 St 估计。这意味着必须为组内协方差矩阵估计的参数数目是 Tp(p+1)/2,必须为均值估计的参数数目是 Tp。必须估计的参数总数是 Tp(p+3)/2。
组样本大小相对于 p 很小时,组内协方差矩阵的估计值倾向于很不稳定。判别得分受组内协方差矩阵的逆矩阵的最小特征值影响很大。请参见 Friedman (1989)。因此,若您的组样本大小相对于 p 来说很小,您可能要考虑正则判别方法中所述的“正则”方法。
组 t 的成员关系的后验概率为:
观测 y 被分配给具有最大后验概率的组。
|
SqDist[<组 t>]
|
|
|
Prob[<组 t>]
|
|
|
Pred <X>
|
|
•
|
参数 λ 权衡分配给合并的协方差矩阵和组内协方差矩阵(不假定相等)的权重。
|
|
•
|
参数 γ 确定向对角矩阵的收缩量。
|
对于正则方法,组 t 的协方差矩阵为:
按以下方式计算组 t 的成员关系的后验概率:
观测 y 被分配给具有最大后验概率的组。
|
SqDist[<组 t>]
|
|
|
Prob[<组 t>]
|
|
|
Pred <X>
|
当您有很多协变量特别是协变量数超过观测数 (p > n) 时,“宽线性”方法很有用。该方法的核心是高效计算合并的组内协方差矩阵 Sp 的逆矩阵或它的转置矩阵(若 p > n)。它使用奇异值分解方法来避免为大的协方差矩阵反转和分配空间。
请参见“保存公式”选项给出的公式符号了解相关符号。“宽线性”计算步骤如下所示:
|
1.
|
|
2.
|
|
3.
|
|
5.
|
|
6.
|
|
7.
|
则 R 可以表示为:
|
8.
|
然后按以下方式定义 R 的平方根倒数:
|
9.
|
当您保存公式时,Mahalanobis 距离以分解的形式给出。对于观测 y,到组 t 的平方距离如下所示,其中最后一个等式中的 SqDist[0] 和 Discrim Prin Comp 在保存的公式中定义:
|
SqDist[<组 t>]
|
|
|
Prob[<组 t>]
|
|
|
Pred <X>
|
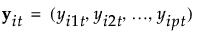

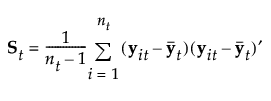
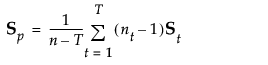
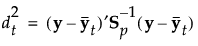
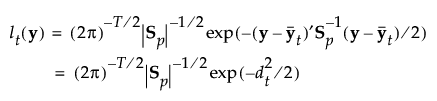
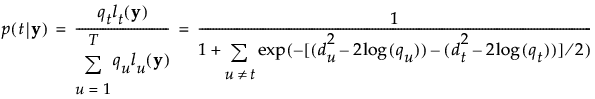
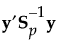
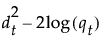
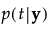
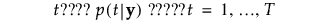
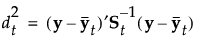
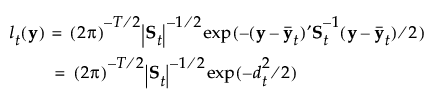
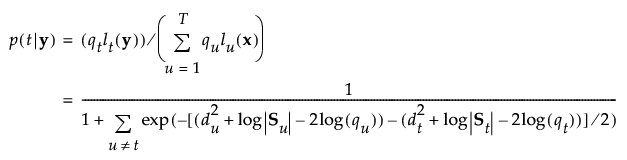
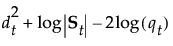
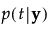
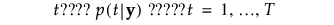
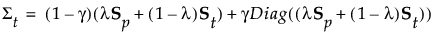
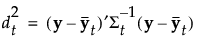
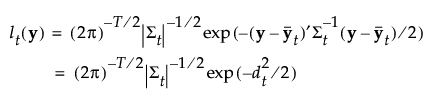
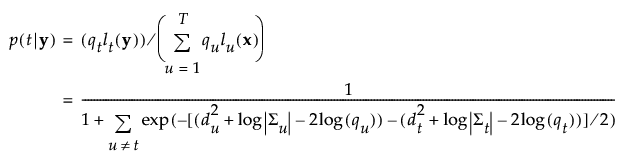
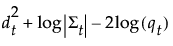
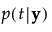
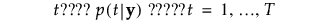
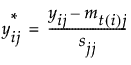
 值的矩阵。
值的矩阵。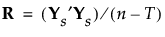
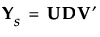
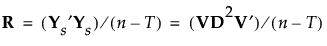
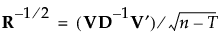
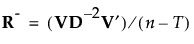
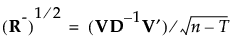
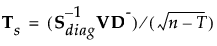
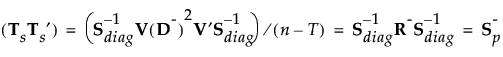
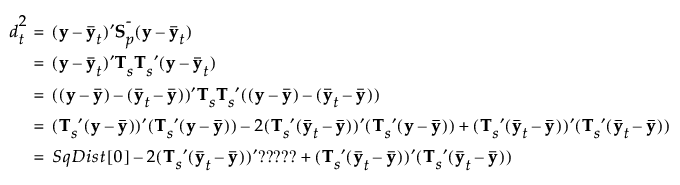
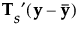 给出,其中
给出,其中 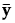 是包含总均值的
是包含总均值的 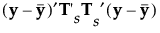
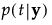 ,在
,在