|
μ = b0 + b1 * f(time)
|
|
|
μ = b1 * f(time)
|
|
|
μ = b0X + b1 * f(time)
|
|
|
μ = b1X * f(time)
|
|
|
μ = b0 + b1X * f(time)
|
|
|
μ = b0 - b1 * Exp[-b2 * Exp[b3 * [Arrhenius(X0) - Arrhenius(X)]] * f(time)]
|
|
|
μ = b0 * [1 - Exp[-b1 * Exp[b2 * [Arrhenius(X0) - Arrhenius(X)]] * f(time)]]
|
|
|
μ = b0 + b1 * Exp[-b2 * Exp[b3 * [Arrhenius(X0) - Arrhenius(X)]] * f(time)]
|
|
|
μ = b0 * Exp[-b1 * Exp[b2 * [Arrhenius(X0) - Arrhenius(X)]] * f(time)]
|
|
|
μ = b0 ± Exp[b1 + b2 * Arrhenius(X)] * f(time)
|
|
|
μ = b0 ± Exp[b1 + b2 * Log(X)] * f(time)
|
|
|
μ = b0 ± Exp[b1 + b2 * X] * f(time)
|
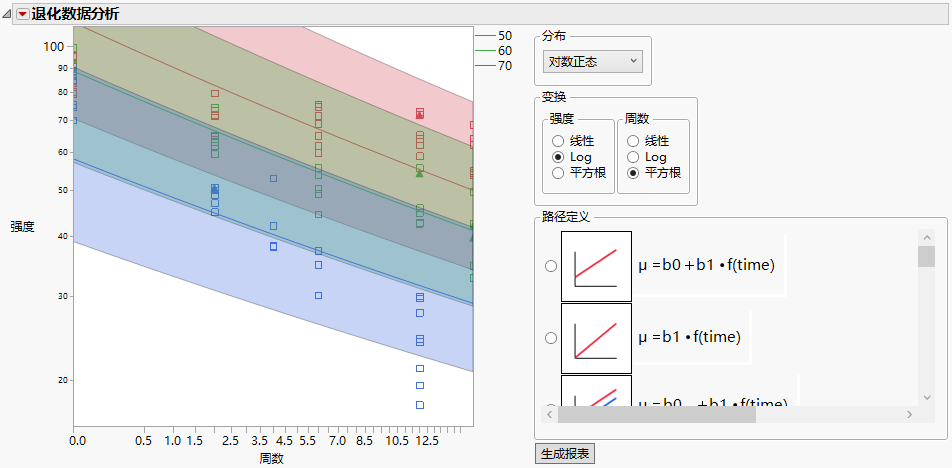
图 8.12 使用对数正态分布的共同斜率模型
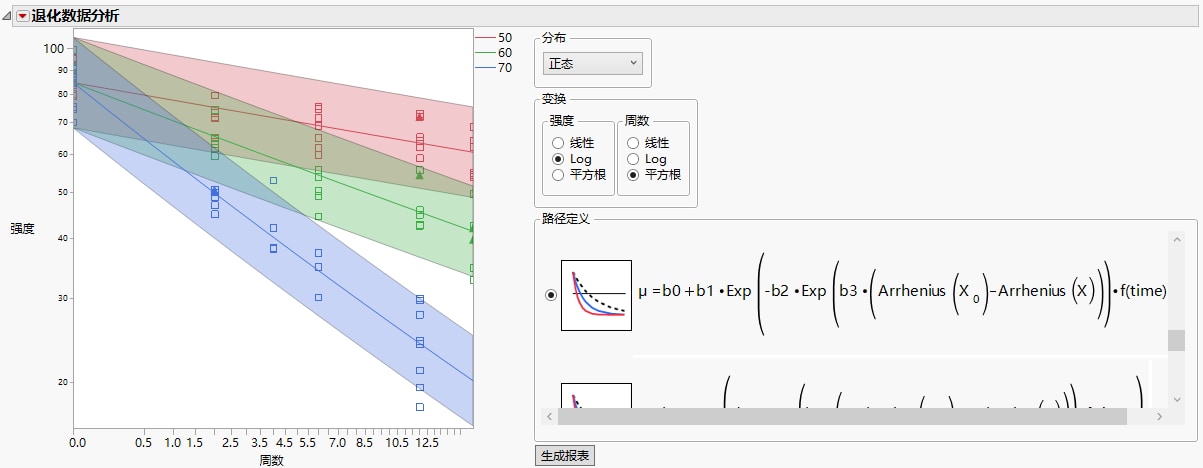
首次选择以上任意模型时,您需要指定温度的测量值尺度,并为 X0(典型使用条件下的温度)指定一个值。X0 的值用于构造时间加速因子 (Meeker and Escobar, 1998)。若您随后选择另一个一阶动力学模型或 Arrhenius 速率模型(请参见Arrhenius 速率),该平台会记住并使用这些指定内容。
图 8.13 一阶动力学 3 型模型的示例
该模型是 3 型模型的垂直偏移版本。在线性尺度上,当时间趋向于无穷大时,曲线在 0 处具有下渐近线。